Многокритериальные задачи оптимизации показателей качества

Раздел 5.Многокритериальные задачи оптимизации показателей качества

Общая задача принятия решений состоит в том, из множества возможных решений выбирается одно решение, оптимальное для данных условий. Выбор при этом производит эксперт – лицо, принимающее решение (ЛПР), который задает приоритеты исходя из своих целей и предпочтений. С точки достижения определенной цели каждое из возможных решений можно охарактеризовать эффективностью, степенью достижения цели. У эксперта в зависимости от его предпочтений складывается определенное представление о достоинствах и недостатках выбираемого решения и с учетом этих представлений одно решение он предпочитает другому.

Следовательно, оптимальное решение – это решение, которое с точки зрения эксперта предпочтительнее других возможных решений и в данном случае понятие оптимальности решения обусловлено предпочтениями ЛПР.

Формулирование предпочтений ЛПР в математическом выражении представляет с одной стороны сложную, а с  другой – необходимую для нахождения оптимального решения задачу. Поэтому теория принятия решений направлена на разработку методов, позволяющих в рамках математической модели выразить предпочтения эксперта. Это позволяет найти обоснованную процедуру выбора оптимального решения. С этой целью осуществляется моделирование процессов принятия решения. Для формализации процесса нахождения оптимального решения необходимо, чтобы задача хорошо изучена и в достаточной степени структурирована. При слабой структурированности задачи формализация трудно осуществима и чаще используется метод последовательного перебора.

В многокритериальных задачах оптимизации заданы не одна, а одновременно несколько целевых функций (критериев). Поэтому многокритериальные задачи наряду со множеством X допустимых решений (альтернатив) х € Rⁿ, X € Rⁿ,  характеризуются набором целевых функций f₁,

f₂, … ,f_m , заданных на множестве Х. Если m > 1, то существует набор целевых функций, образующих вектор-функцию. Обозначим её как f(x) = (f₁(x), f₂(x), …,f_m(x)). Рассмотрим также множество оценок Y, элементами которого являются оценки у = f(x). Каждому решению х, принадлежащему множеству Х соответствует одна оценка у = f(x), принадлежащая множеству оценок Y, а каждой оценке у из множества Y соответствует не менее, чем одно решение х из множества Х, для которых f(x) = y.

          Пространство Rⁿ, которое содержит множество решений Х называется пространством решений, а пространство R^m, в котором задано множество оценок, называется пространством оценок или критериальным пространством.

          Множество решений и множество оценок взаимосвязаны и выбор решения х из множества Х означает выбор соответствующей оценки у из множества оценок Y.

          В процессе принятия решения осуществляются действия над множеством решений (альтернатив), которые позволяют выделить подмножество или одну альтернативу, т. е. сужать множество решений. Для этого необходимо произвести сравнение альтернатив между собой и определить наиболее предпочтительные альтернативы. Множество решений может быть в общем случае конечным, счетным или континуальным, а оценка решений может осуществляться по ряду критериев как количественного, так и качественного характера. Выбор может осуществляться в условиях определенности и может иметь вероятностный характер.

          Если х – некоторое решение из множества Х, f(x) – целевая функция (критерий качества, функция предпочтения, функция полезности и т. д.), то в том случае, когда f(x₁) > f(x₂) решение x₁ предпочтительнее решения x₂ и наоборот. Когда выбор осуществляется в условиях определенности (выбор любого решения влечет однозначный результат), а целевая функция численно выражает оценку данного действия, то наилучшим решением х^* является то, которое обладает наибольшим значением критерия

x^* = arg max f(х)

     х € Х

          Когда для оценивания альтернатив используются несколько целевых функций f(x_i) i = 1, 2, …m, то может в принципе быть такой случай, когда на множестве решений существует такое, которое обладает наибольшими оценками по всем критериям. Это решение и является наилучшим. Но если такого решения нет, то возникает проблема неоднозначности выбора. Для устранения неоднозначности используются различные способы решения многокритериальных задач. Наиболее употребительным из них является способ сведения многокритериальной задачи к однокритериальной. Он заключается во введении обобщенного критерия (суперкритерия), который является скалярной функцией векторного аргумента

f₀(x) = f₀(f₁(x), f₂(x), … f_m(x))

Обобщенный критерий позволяет упорядочить решения по значениям f₀(x) и выделить наилучшее решение.

Поэтому для принятия решения в многокритериальной задаче оптимизации необходима определенная информация о предпочтениях ЛПР. Рассмотрим далее случаи, когда дополнительная информация о предпочтениях заключается в том, что известна относительная значимость оценок. В этом случае для нахождения оптимального решения используются методы, основанные на свертках различного типа.

          Одним из наиболее употребительных способов преодоления неопределенности целей является представление обобщенного критерия в виде линейной (аддитивной) свертки:

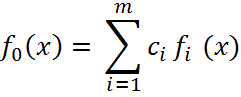
где с_i – весовые коэффициенты, .

          Наряду с аддитивной сверткой применяется также мультипликативная свертка вида:

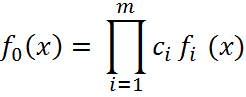
Весовые коэффициенты  определяются экспертными методами и отражают предпочтения ЛПР. Устранение неопределенности целей в данном случае достигается их ранжированием на основе применения метода экспертных оценок.

          Другим методом устранения неопределенности целей является использование пороговых (контрольных) критериев. Он заключается в том, что задается система нормативных значений критериев f₁^*,f₂^*,…, f_i^*,…,f_N^* , а ограничения задачи имеют вид:

f_i  ≥  f_i^*, I = 1,2, …N

          Целевая функция определяется в виде:

f(x) = min f_i(x)/ f_i^*

Задача заключается в нахождении решения

x^* = arg max f(х)

     х € Х

          Метод использования главного критерия предполагает, что введена система нормативных значений критериев f₁^*,f₂^*,…, f_i^*,…,f_N^*, а система ограничений имеет вид: