«Оптимизация показателей качества»
Курсовая работа
Выполнил студент: Завьялова Н.С.
Факультет: ФРЭ
Курс: V
Специальность: 1908
Шифр: 25-0138
Проверил:
Санкт-Петербург
2007г.
Задание №1
Задание: Из трех видов сырья производится два вида продукции. Прибыль от реализации одной единицы продукции первого типа составляет α1 тыс. руб., а второго – α2 тыс. руб. Запас сырья каждого вида составляет β1, β2, β3 единиц соответственно. Потребность в сырье для изготовления продукции первого типа составляет Р11 единиц сырья первого вида, Р12 единиц сырья второго вида, Р13 единиц сырья третьего вида, а для изготовления продукции второго типа – Р21 единиц сырья первого вида, Р22 единиц сырья второго вида, Р23 единиц сырья третьего вида. Для каждого типа изделий определить такой объем производства Х1 и Х2, который обеспечивает максимальную прибыль от реализации изготовленной продукции при условии не превышения запасов имеющегося сырья. Задачу решить симплексным методом путем преобразования симплекс – таблиц.
Исходные данные:
Р11=13 ед.
Р12=9 ед.
Р13=8 ед.
Р21=7 ед.
Р22=10 ед.
Р23=11 ед.
β1= 120 ед.
β2= 110 ед.
β3= 100 ед.
α1=6 тыс. руб.
α2=8 тыс. руб.
Решение:
Составим математическую модель задачи. Искомый выпуск продукции 1-го вида обозначим через Х1, выпуск продукции 2-го вида – Х2. Т.к. на выделенный предприятию фонд сырья каждого вида имеются ограничения переменные Х1 и Х2 должны удовлетворять следующей системе неравенств:
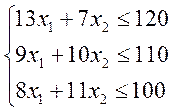
Общая стоимость произведенной предприятием продукции:
F=6х1+8х2
По своему экономическому содержанию переменные Х1 и Х2 могут принимать только неотрицательные значения:
Х1, Х2≥0
Переходим от ограничений – неравенств к ограничениям – равенствам. Введем три дополнительные переменные, по экономическому смыслу означающие не используемое при данном плане производства количество сырья того или иного вида:
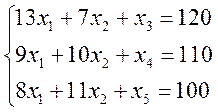
Составим симплекс – таблицу для I итерации (табл.1).
Таблица 1
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
||
|
Y |
0 |
6 |
8 |
0 |
0 |
0 |
|
Х3 |
120 |
13 |
7 |
1 |
0 |
0 |
|
Х4 |
110 |
9 |
10 |
0 |
1 |
0 |
|
Х5 |
100 |
8 |
11* |
0 |
0 |
1 |
Первая итерация.
Шаг 1 (выбор ведущего столбца)
Т.к. в нулевой строке имеются положительные элементы, то исходное допустимое базисное решение
Х1=0, Х2=0, Х3=120, Х4=110, Х5=100
Не является оптимальным. Из двух положительных элементов нулевой строки выбираем максимальный а02=8 и таким образом второй столбец является ведущим.
Шаг 2 (выбор ведущей строки)
В ведущем столбце имеется три положительных элемента а12=9, а22=10, а32=11.
Сравнивая
отношения 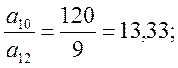
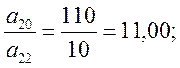
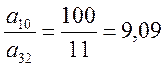 выбираем минимальное
выбираем минимальное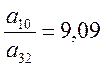 . Таким образом, третья строка –
ведущая, а ведущий элемент - а32.
. Таким образом, третья строка –
ведущая, а ведущий элемент - а32.
Шаг 3 (преобразование системы к диагональному виду относительно нового набора базисных переменных)
Ведущий элемент - а32, поэтому переменную Х5 следует вывести из базиса, а вместо нее ввести переменную Х2.
Третью строку умножаем последовательно на -8/11, -7/11, -10/11 и получившиеся строки складываем соответственно с нулевой, первой и второй. Все элементы ведущего столбца (кроме ведущего элемента) станут нулевыми и симплекс – таблица во второй итерации примет вид:
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
||
|
Y |
-800/11 |
2/11* |
0 |
0 |
0 |
-8/11 |
|
Х3 |
620/11 |
87/11 |
0 |
1 |
0 |
-7/11 |
|
Х4 |
210/11 |
19/11 |
0 |
0 |
1 |
-10/11 |
|
Х2 |
100/11 |
8/11 |
1 |
0 |
0 |
1/11 |
Вторая итерация.
Шаг 1.
В нулевой строке имеется единственный положительный элемент а01=2/11 и следовательно ведущий столбец определяется однозначно.
Шаг 2.
В качестве
ведущей строки сравнивая отношения коэффициентов 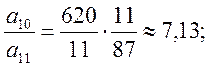
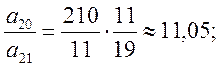
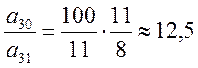 выбираем
минимальное
выбираем
минимальное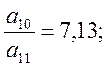 . Таким образом, а ведущий элемент –
а11=7,13.
. Таким образом, а ведущий элемент –
а11=7,13.
Шаг 3
Переменную Х3 вывести из базиса и ввести переменную Х1. Для этого первую строку умножаем последовательно на (-2/87), (-19/87), (-8/87) и складывая получившиеся строки соответственно с нулевой, второй и третьей строками придем к оптимальной таблице:
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
||
|
Y |
-68360/957 |
0 |
0 |
-2/87 |
0 |
-682/957 |
|
Х1 |
620/87 |
1 |
0 |
11/87 |
0 |
-7/87 |
|
Х4 |
6490/957 |
0 |
0 |
-19/87 |
1 |
-737/957 |
|
Х2 |
3740/957 |
0 |
1 |
-8/87 |
0 |
143/957 |
В этой таблице в нулевой строке нет положительных элементов, текущее базовое решение
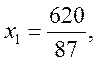
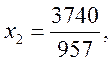
![]()
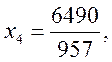
![]()
является оптимальным и соответственно максимальное значение прибыли:
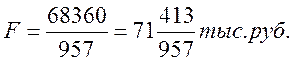
Задание №2
Задание: Дана задача нелинейного программирования. Найти максимум и минимум целевой функции графоаналитическим методом. Составить функцию Лагранжа и показать, что в точках экстремума выполняются достаточные условия минимума (максимума).
Исходные данные:
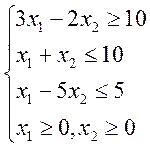
![]()
А=1
В=3
Таким образом:
![]()
Решение:
Областью
допустимых решений задачи является четырехугольник ABCD
(рис.1). Полагая значение целевой функции равным некоторому числу h получаем линии уровня, а именно окружности ![]() с центром Е (2;5) и радиусом
с центром Е (2;5) и радиусом ![]() . С увеличением (уменьшением) числа h соответственно увеличиваются (уменьшаются) значения функции
F.
. С увеличением (уменьшением) числа h соответственно увеличиваются (уменьшаются) значения функции
F.
Минимальное и максимальное значения определим, проводя из точки Е окружности разных радиусов. На рис.1 видно, что максимальное значение функция принимает в точке D, а минимальное – в т. К.
Определим координаты точки максимума целевой функции как координаты точки пересечения прямых:
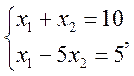
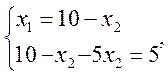
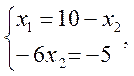
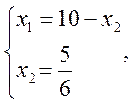
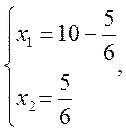
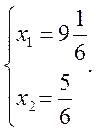
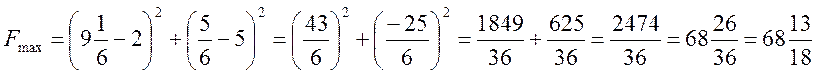
Определим
координаты точки минимума целевой функции. Для нахождения координаты т. К
приравняем угловые коэффициенты прямой ![]() и
касательной к окружности в т. К.
и
касательной к окружности в т. К.
Из уравнения ![]() найдем, что
найдем, что 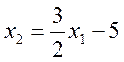 ,
а угловой коэффициент равен
,
а угловой коэффициент равен ![]() . Угловой
коэффициент касательной к окружности в т.К можно получить как значение
производной функции Х2 по переменной Х1 в этой точке.
. Угловой
коэффициент касательной к окружности в т.К можно получить как значение
производной функции Х2 по переменной Х1 в этой точке.
![]()
![]()
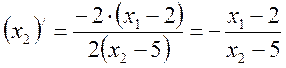
Из равенства угловых коэффициентов получим одно из уравнений для определения координаты т. К
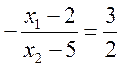
![]()
![]()
![]()
Присоединяя к
нему уравнение прямой ![]() получим систему уравнений:
получим систему уравнений:
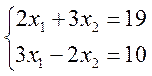 ,
,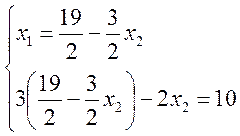 ,
,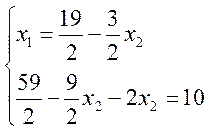 ,
,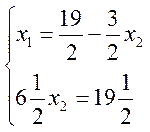 ,
,
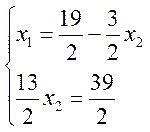 ,
,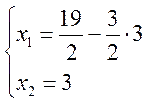 ,
,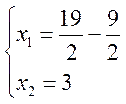 ,
,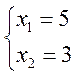 .
.
![]()
Таким образом,
![]() ,
, 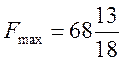 .
.
Задание №3
Задание: Двум предприятиям выделяют средства в количестве d единиц. При выделении первому предприятию на год x единиц средств оно обеспечивает доход k1x единиц, а при выделении второму предприятию у единиц средств, оно обеспечивает доход k1у единиц. Остаток средств к концу года для первого предприятия равен nx, а для второго my. Как распределить все средства в течение 4-х лет, чтобы общий доход был наибольшим. Задачу решить методом динамического программирования.
Исходные данные:
А=2200
k1=2
k2=1
n=0,3
m=0,5
Решение:
Весь период длительностью 4 года разбиваем на 4 этапа, каждый из которых равен одному году. Пронумеруем этапы начиная с первого года. Пусть Хk и Yk – средства, выделенные соответственно предприятиям А и В на k –том этапе. Тогда сумма Хk + Yk =аk является общим количеством средств, используемых на k –том этапе и оставшиеся от предыдущего этапа k – 1. на первом этапе используются все выделенные средства и а1 =2200 ед. доход, который будет получен на k –том этапе, при выделении Хk и Yk единиц составит 2Хk + 1Yk . пусть максимальный доход, полученный на последних этапах начиная с k –того этапа составляет fk (аk) ед. запишем функциональное уравнение Беллмана, выражающее принцип оптимальности: каково бы не было начальное состояние и начальное решение последующее решение должно быть оптимальным по отношению к состоянию, получаемому в результате начального состояния:
fk (аk)=max [ 2х+y + fk+1 (аk+1)]
для каждого этапа нужно выбрать значение Хk , а значение Yk =аk - хk. С учетом этого найдем доход на k –том этапе:
2хk+yk=2хk+ аk - хk=хk+ аk n m
аk=0,3хk-1+0,5 yk-1=0,3хk-1+0,5(аk-1 - хk-1)= 0,3хk-1+0,5аk-1 -0,5 хk-1=0,5аk-1-0,2хk-1
Функциональное уравнение Беллмана будет иметь вид:
fk (аk)=max [аk+хk+fk+1(аk+1)]
Рассмотрим все этапы, начиная с последнего.
При k=4.
F4 (а4)=max [а4+х4+0]=2а4, (т.к. максимум линейной функции а4 + х4 достигается в конце отрезка [0;а4] при х4 = а4) y4=х4-а4=0.
а4=0,5а3-0,2х3
При k=3.
F3 (а3)=max [а3+х3+2(0,5а3-0,2х3)]= max [а3+х3+а3–0,4х3)]= max [2а3+0,6х3]=2,6а3, (т.к. максимум линейной функции 2а3 +0,6 х3 достигается в конце отрезка [0;а3] при х3 = а3) y3=х3-а3=0.
а3=0,5а2-0,2х2
При k=2.
F2(а2)=max[а2+х2+2,6(0,5а2-0,2х2)]=max[а2+х2+1,3а2–0,52х2)]=
=max [2,3а2+0,48х2]=2,78а2 , (т.к. максимум линейной функции 2,3а2 +0,48 х2 достигается в конце отрезка [0;а2] при х2 = а2) y2=х2-а2=0.
а2=0,5а1-0,2х1
При k=1.
F1(а1)=max[а1+х1+2,78(0,5а1-0,2х1)]=max[а1+х1+1,39а1–0,556х1)]=
=max [2,39а1+0,444х1]=2,834а1 , (т.к. максимум линейной функции 2,39а1 + 0,444 х1 достигается в конце отрезка [0;а1] при х1 = а1). y1= а1- х1=0.
Таким образом, максимальный доход за 4-е года составит
F1(а1)=2,834*2200=6324,80 ед.
Для получения этого дохода нужно во все четыре года все средства вложить в предприятие А (а1= х1, y1= 0; а2= х2, y2= 0; а3= х3, y3= 0; а4= х4, y4= 0).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.