Оптимизация показателей качества при наличии ограничений. Линейное программирование

2.3. Оптимизация показателей качества при наличии ограничений

Линейное программирование

Определение 1. Общей задачей ЛП называется задача, которая состоит в определении максимального (минимального) значения функции:

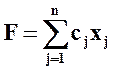                      (2.23)

при условиях

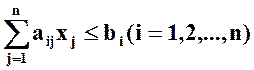   (2.24)

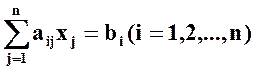  (2.25)

           x_j ≥ 0                 (2.26)

где   а_ij , b_i, c_j – заданные постоянные величины и к ≤ m.

Определение 2. Функция F называется целевой функцией (или линейной формой) задачи (2.23)….(2.26), а условия (2.24)…(2.26) называются ограничениями данной задачи.

Определение 3. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции F при  выполнении условий (2.24) и (2.26),где к = m, l = n.

Определение 4. Основной ( или канонической) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции F при выполнении условий (2.25) и (2.26), где к = 0 и l = n.

Определение 5. Совокупность чисел Х = (х₁, х₂, …., х_n) удовлетворяющих ограничениям задачи (2.23)…(2.26) называется допустимым решением (или планом).

Определение 6. План Х^* = (х_1*, х_2*, …., х_n*), при котором целевая функция задачи (2.23) принимает свое максимальное значение (минимальное) значение, называется оптимальным.

Однофазный симплекс-метод  Рассмотрим каноническую задачу линейного программирования в специальной (диагональной)  форме:

y = с₁ х₁ + с₂x₂+….+ с_nx_n → min

х₁ +                         +  а_1,к+1х_к+1 +….+ a_1n х_n = b₁

                       х₂ +                   + а_2,к+1х_к+1 +….+ a_2n х_n = b₂       (2.27)

………………………………………………………

              x_k +           + а_k,к+1х_к+1 +….+ a_kn х_n = b_k

Обозначим у = х₀ ; b_i = a_i0 и запишем:

                           х₀ - с₁ х₁ - с₂x₂-….- с_nx_n = 0                       (*)

С уравнением (*) сложим все уравнения системы (2.27), умноженные последовательно на с₁, с₂,…,с_к. Получим первое уравнение системы (2.28) в котором отсутствуют все переменные х₁ , х₂ , …., х_к, но в котором может быть свободный член а₀₀:

                     х₀ +                                  +  а_0,к+1х_к+1 +….+ a_0n х_n = а₀₀

х₁ +                         +  а_1,к+1х_к+1 +….+ a_1n х_n = а₁₀

                         х₂ +                       + а_2,к+1х_к+1 +….+ a_2n х_n = а₂₀              (2.28)

………………………………………………………

              x_k +           + а_k,к+1х_к+1 +….+ a_kn х_n = а_k0

где

                                

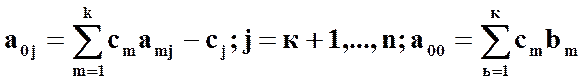
Система (2.28) является диагональной формой относительно переменных   х₀, х₁ , х₂ , …., х_к  (или говорят, что система приведена к диагональному виду относительно этих переменных).

          Решение

                             х_i = a_i0 i = 1, 2, …, k; х_к+1 = …= х_n = 0                     (2.29)

этой системы без учета нулевого уравнения называется базисным решением, а переменные  х₁ , х₂ , …., х_к  - базисными переменными.

          Если среди элементов  а₁₀, а₂₀,… а_k0 имеются нулевые, то соответствующие компоненты базисного решения также равны нулю.

          Вырожденным базисным решением называется базисное решение, хотя бы одна базисная компонента которого равна нулю.

          Систему (2.28)записывают в виде симплекс – таблицы :

                                                                             Таблица 2.1

		х1	х2	…	хk	хk+1	...	хn
х0	a00	0	0	…	0	a0,k+1	…	a0,n
х1	a10	1	0	…	0	a1,k+1		a1,n
х2	a20	0	1	…	0	a2,k+1		a2,n
…	…	…	…	…	…	…	…	…
хk	ak0	0	0	…	1	ak,k+1		ak,n

      Каждая строка таблицы задает соответствующее уравнение системы (2.28), свободный член которого записан в самом левом (ненулевом) столбце.

       Слева от таблицы записаны текущие базовые переменные. Столбцы, соответствующие базисным переменным, составляют единичную подматрицу симплекс - таблицы (Табл.2.1).

       Исходную задачу ЛП можно привести к диагональной форме относительно х₀  и каких-то других к переменных из набора х₁ , х₂ , …., х_n. В этом случае изменяются и базисные переменные, а столбцы, отвечающие этим базисным переменным будут располагаться в соответствующих графах симплекс-таблицы и составлять подматрицу, отличающую от единичной лишь перестановкой столбцов.

       В любом случае текущее базисное решение – это такое решение, в котором все небазисные переменные имеют нулевое значение, а базисные переменные равны соответствующим элементам нулевого столбца.

       Рассмотрим алгоритм симплекс – метода. Начинать следует с таблицы, которая соответствует диагональной форме относительно х₀ и некоторых к (базисных) переменных из полного набора х₁ , х₂ , …,х_n.

Все элементы нулевого столбца (кроме, возможно a₀₀) должны быть неотрицательными, так как  b_i  ≥ 0.

       Шаг 1. Если среди элементов нулевой строки (не считая a₀₀) нет положительных, так как текущее базисное решение оптимально и минимальное значение целевой функции равно a₀₀. Таблица, соответствующая этому случаю называется оптимальной таблицей.

Если таблица не является оптимальной, то среди положительных элементов нулевой строки (кроме a₀₀) следует выбрать некоторый элемент. Обычно среди положительных элементов выбирают максимальный, но это не обязательно. Пусть выбран элемент a_0к > 0. Тогда столбец с номером s называется ведущим столбцом.

      Если все элементы нулевой строки таблицы не положительны, то значение целевой функции  х₀ найденное из нулевого уравнения, является разностью между a₀₀ и суммой произведений небазисных переменных на соответствующие коэффициенты: х₀ = a₀₀  - ∑ a_0j х_j (так как коэффициенты при базисных переменных равны нулю). Таким образом величина х₀ зависит только от небазисных переменных. Коэффициенты a_0j не положительны, а небазисные переменные не отрицательны. Поэтому минимальное значение х₀ достигается только в том случае, когда значения всех небазисных переменных равны нулю. Следовательно, число х₀ = a₀₀ действительно минимум, а текущее базисное решение является оптимальным. Следует отметить, что выбор максимального элемента нулевой строки на шаге 1 обеспечивает максимальное убывание целевой функции и, таким образом, ведет к сокращению общего числа вычислений.

       Шаг 2. Выделить среди положительных элементов  ведущего столбца элемент a_is, для которого отношение  a_i0 / a_is  является наименьшим.

Пусть этот элемент a_rs Его называют ведущим элементом, строку с номером r – ведущей строкой. При выполнении вычислений шага 2 предполагается, что в ведущем столбце найдется по крайней мере один положительный элемент. Если это предположение не выполняется, т.е. все элементы ведущего столбца  (кроме a_0s) не положительны, то исходная задача не имеет конечного решения (целевая функция не ограничена снизу на допустимом множестве).

        Чтобы убедиться в этом, предположим, что симплекс – таблица имеет вид таблицы 1 и s = n. Тогда решение

              х_i (ג) = a_i0 - a_in ג ,  i=1,2,…k;  х_i (ג) = 0, i = k+1, … n-1; х_i (ג) = ג

так, как a_i0 ≥ 0;  a_in  ≤ 0, I = 1,2,…, k при любых ג ≥ 0 является допустимым, т. е. удовлетворяет соответствующей системе уравнений и имеет неотрицательные компоненты.