Промышленность \ Оптимизация показателей качества

Оптимизация показателей качества при наличии ограничений. Линейное программирование, страница 2

Из нулевой строки таблицы 1 имеем:

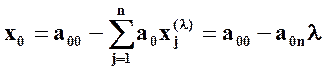
так, как a₀_n > 0, отсюда следует, что увеличивая ג можно неограниченно уменьшить значение целевой функции.

При выполнении шага 2 может оказаться, что минимум отношения a_i₀ / a_is (a_is > 0), будет одинаковым для нескольких строк таблицы, (нескольких i), т. е. сразу несколько строк таблицы могут быть ведущими. В этом случае выбирают строку с меньшим номером. Такое правило теоретически может приводить к зацикливанию. Задачи в этом случае называют вырожденными. Шаг 3. Используя элементарные преобразования сделать так, чтобы ведущий элемент a_rs стал равным единице, а остальные элементы ведущего столбца – нулевыми, т.е. преобразовать систему к диагональному виду относительно нового набора базисных переменных.

Новый набор отличается от прежнего тем, что в нем вместо переменной х_r участвует переменная х_s. Поэтому базисную переменную х_r слева от таблицы следует заменить на х_s. После этого вернуться к шагу 1.

Последовательное выполнение вычислений шагов 1-3 составляет одну итерацию симплекс-метода.

Итерации выполняют до тех пор, пока среди элементов нулевой строки (не считая a₀₀) не окажется ни одного положительного элемента. Тогда текущее базисное решение является оптимальности, а минимальное значение целевой функции равно левому верхнему элементу таблицы.

Если целевая функция не является ограниченной снизу на допустимом множестве, то на одном из шагов 2 будет получен ведущий столбец, в котором нет ни одного положительного элемента (не считая элемента нулевой строки).

Замечание 1 Алгоритм СМ обладает тем свойством, что после выполнения некоторого конечного числа итераций, либо будет найдено оптимальное решение, либо установлена неразрешимость задачи.

Замечание 2 На каждой итерации СМ сохраняется допустимость базисного решения, т.е. элементы нулевого столбца, (не считая верхнего) все время остаются неотрицательными. Это свойство следует из следует из правила выбора ведущей строки на шаге 2.

Значение целевой функции на каждой итерации уменьшается на величину a_r₀ / a_rs: а₀₀ – a_r₀ / a_rs.

Пример. F = - 2 х₁ – х₂ + х₃ - х₄ + х₅ → min

х₁ + х₂ +х₃ = 5

2 х₁ + х₂ +х₄ = 9

х₁ + 2 х₂ +х₅ = 9

Исходное допустимое базисное решение:

х₁ = 0, х₂ = 0, х₃ = 5, х₄ = 9, х₅ = 7

Обозначим х₀ = F и составим уравнение (*). C уравнением (*) сложим уравнения ограничений, умноженные соответственно на +1, -1, +1.

х₀ + 2 х₁ + х₂ - х₃ + х₄ - х₅ = 0 (*)

х₁ + х₂ +х₃ = 5 (+1)

2 х₁ + х₂ +х₄ = 9 (-1)

х₁ + 2 х₂ +х₅ = 9 (+1)

Получим первое уравнение системы (2.28) в виде 2х₁ +3х₃ = 3 и составим начальную симплекс – таблицу (табл.2.2):

Таблица 2.2.

		х₁	х₂	х₃	х₄	х₅
х₀	3	+2	+3	0	0	0
х₃	5	1	1	1	0	0
х₄	9	2	1	0	1	₀
х₅	7	1	2	0	0	1

В нулевой строке имеются положительные элементы. Поэтому текущее решение не является оптимальным. Среди двух неравных положительных элементов нулевой строки выбираем максимальный

a₀₂= +3. Ведущий столбец – второй. В этом столбце выбираем минимум из отношений min {7/2; 9/1; 5/1} = 7/2, а ведущим элементом выбираем a₅₂= 2.

Таким образом переменную х₅ следует вывести из базиса, а вместо нее ввести переменную х₂. Для этого умножим последнюю строку на -3/2, -1/2, -1/2 и складываем соответственно с нулевой, первой и второй строками и запишем соответствующую симплекс – таблицу (Табл.2.3):

Таблица 2.3

		х₁	х₂	х₃	х₄	х₅
х₀	-15/2	+1/2	0	0	0	-3/2
х₃	3/2	½^*	0	1	0	- 1/2
х₄	11/2	3/2	0	0	1	- 1/2
х₅	7/2	1/2	1	0	0	1/2

В первой строке один положительный элемент и таким образом ведущий столбец – первый. Сравнивая отношения найдем минимум

min {3/2: 1/2; 11/2: 3/2; 7/2:1/2} = 3/2:1/2 = 3.

Это значит, что переменную х₃ следует вывести из базиса и ввести вместо нее переменную х₁. Для этого умножим первую строку на (-1), (-3), и (-1) и сложим ее соответственно с нулевой, второй и третьей строкой и запишем соответствующую симплекс – таблицу (2.4):

Таблица 2.4.

		х₁	х₂	х₃	х₄	х₅
х₀	-9	0	0	-1	0	-1
х₃	3	1	0	2	0	-1
х₄	1	0	0	-3	1	1
х₅	2	0	1	-1	0	1

Таким образом минимальное значение F = -9, а оптимальный план

х₁ = 3, х₂ = 2, х₃ = 0, х₄ = 1, х₅ = 0.

Двухфазный симплекс-метод Рассмотрим общую (не приведенную к диагональному виду) задачу линейного программирования в каноническом виде:

y = с₁ х₁ + с₂x₂+….+ с_nx_n → min

a₁₁х₁ + а₁₂х₂+….+ a₁_n х_n = b₁

a₂₁ х₁ + а₂₂х₂₂+….+ a₂_n х_n = b₂ (2.29)

………………………………

a_к1 x_k + а_k₂х₂+….+ a_kn х_n = b_k

х₁, х₂,…, х_n ≥ 0, b_i ≥ 0.

1. Введем дополнительные неотрицательные переменные х_n₊₁, х_n₊₂,…, х_n_+к, которые называются искусственными переменными и рассмотрим новую задачу:

z = х_n₊₁ + х_n₊₂ +…+ х_n_+к → min

y - с₁ х₁ - с₂x₂-….- с_nx_n = 0

a₁₁х₁ + а₁₂х₂+….+ a₁_n х_n + х_n₊₁ = b₁

a₂₁ х₁ + а₂₂х₂₂+….+ a₂_n х_n + х_n₊₂ = b₂ (2.30)

………………………………

a_к1 x_k + а_k₂х₂+….+ a_kn х_n + х_n_+к = b_k

х₁, х₂,…, х_n, х_n_+к ≥ 0, b_i ≥ 0.

2. Складывая уравнение z - х_n₊₁ - х_n₊₂ -…- х_n_+к= 0 со всеми уравнениями, содержащими переменные х_n₊₁, х_n₊₂,…, х_n_+к, получим систему:

d₁х₁ + d₂х₂+….+ d_n х_n +z =z₀

- с₁ х₁ - с₂x₂-….- с_nx_n +y = 0

a₁₁х₁ + а₁₂х₂+….+ a₁_n х_n + х_n₊₁ = b₁

a₂₁ х₁ + а₂₂х₂₂+….+ a₂_n х_n + х_n₊₂ = b₂ (2.31)

………………………………

a_к1 x_k + а_k₂х₂+….+ a_kn х_n + х_n_+к = b_k

х₁, х₂,…, х_n, х_n_+к ≥ 0, b_i ≥ 0

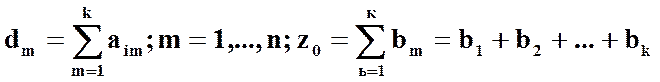
Система (2.31) имеет диагональный вид относительно переменных z, y, х_n₊₁,…, х_n₊_k. К ней можно применить рассмотренный ранее симплекс – метод. Так как все искусственные не отрицательны, то минимальное значение функции z = х_n₊₁ + х_n₊₂ +…+ х_n_+к = 0. Таким образом, если исходная система ограничений в системе (1) совместна, то значение z_min = 0, будет достигнуто и при этом все искусственные переменные должны стать равными нулю. Вместо них в число базисных переменных войдут переменные из числа х₁, х₂,…, х_n. Затем первую строку системы (2.31) можно вычеркнуть и переходить к минимизации функции y. Такой способ решения исходной канонической задачи называется двухфазным симплекс – методом.

1 2 3

Скачать файл