Оптимизация показателей качества с использованием нелинейного программирования

Раздел 3. Оптимизация показателей качества с использованием нелинейного программирования

3.1. Графоаналитический метод решения задач нелинейного программирования.

          Рассмотрим задачу нелинейного программирования, которая заключается в том, чтобы определить максимальное (минимальное) значение функции n переменных

F(х₁,х₂,….,х_n)                                            (3.1)

при ограничениях вида

f_i (х₁,х₂,….,х_n) = a_i         (i = 1,2, …p)       (3.2)

f_i (х₁,х₂,….,х_n) ≤ a_i         (i = p+1,…m)       (3.3)

где F(х₁,х₂,….,х_n) и  f_i (х₁,х₂,….,х_n) известные функции, по крайней мере одна из которых является нелинейной, a_i – заданные числа.

          Решением задачи являются координаты точки Х^* =(х^*₁,х^*₂,… х^*_n), при которых достигается экстремальное значение функции F(х₁,х₂,….,х_n) и выполняются ограничения задачи (3.2), (3.3).

          Если на переменные наложены условия неотрицательности, то эти условия также включаются в ограничения (3.2), (3.3).

          Для решения задачи (3.1), (3.2), (3.3) необходимо определить область допустимых решений и найти точку внутри или на границе этой области, через которую проходит гиперповерхность экстремального уровня F(х₁,х₂,….,х_n) = d_экстр.

 Графоаналитическое решение задач нелинейного программирования осуществляется в следующей последовательности:

1. Исходя из ограничений (3.2), (3.3) определяется область допустимых решений задачи.

2. На основе (3.1) придавая различные постоянные значения функции F(х₁,х₂,….,х_n) = dстроятся гиперповерхности разных уровней.

3. Находят гиперповерхность экстремального уровня, которая имеет d_maxили d_minи определяется координата точки из области допустимых значений, через которую проходит эта гиперповерхность.

4. Подставляя координаты этой точки в (1) получают решение задачи – максимальное или минимальное значение целевой функции.

Пример 1. Найти максимальное значение функции

                              F =  х₁ – ( х₂ )² + 4 х₂                       (3.4)

при условиях:             2х₁ + 3 х₂  ≤ 30                     (3.5)

 х₁ + 2 х₂  ≤ 18                   (3.6)

 3 х₁ + 2 х₂ ≤ 30                 (3.7)

 х₁ ≤ 7 ,  х₁ , х₂ ≥ 0             (3.8)

Решение. Задача (3.4)…(3.8)  является задачей нелинейного программирования, так как целевая функция (1) является нелинейной.

1. Выделяем область допустимых решений задачи. . Строим прямые, определяя точки пересечения с осями координат:

2 х₁ + 3 х₂ = 30; →  [(х₁=0; х₂ =10); (х₁=15; х₂=0)]

х₁ + 2 х₂ = 18; → [(х₁=0; х₂=9); (х₁=18; х₂=0)]

3 х₁ + 2 х₂ = 30; → [(х₁=0;, х₂=15); (х₁=10; х₂=0)]

х₂ = 7;  → [(х₁=7; х₂=0) ]

Этой областью в плоскости х₁ , х₂ является многоугольник ОАВСД (Рис.3.1).

2. Исходя из (3.4) придавая различные постоянные значения  функции

F =х₁– ( х₂ )² + 4 х₂ = d строим линии уровня для различных значений d:

d = 5, х₁ = 1; d = 4, х₁ = 0; d = 8, х₁ = 4.

3. Находим линию уровня, которая имеет максимальное значение d и определяем координаты точки Е из области допустимых значений, через которую проходит эта линия: х₁ = 7; х₂ = 2.

4. Подставляем координаты точки Е в (3.4) и вычисляем максимальное значение целевой функции F_max = 11 (Рис.3.1).

Пример 2.Найти максимальное и минимальное значение функции

F = (X₁ – 3)² + (X₂ – 4)²          (3.9)

при условиях:                   3 X₁ –  2 X₂ ≤ 24;            (3.10)

                                           3 X₁ +  2 X₂ ≥ 6;             (3.11)

                                            - X₁ + 3 X₂ ≤ 12;            (3.12)

                                                    X₁ ,X₂ ≥ 0              (3.13)

Решение. Задача (3.9)…(3.13)  является задачей нелинейного программирования, так как целевая функция (3.9) является нелинейной.

1. Выделяем область допустимых решений задачи. . Строим прямые, определяя точки пересечения с осями координат:

3 х₁ - 2 х₂ = 24; →  [(х₁=0; х₂ = -12); (х₁= 8; х₂=0)]

х₁ + 2 х₂ = 18; → [(х₁=0; х₂=3); (х₁= 2; х₂=0)]

3 х₁ + 2 х₂ = 30; → [(х₁=0;, х₂= 4); (х₁= - 12; х₂=0)]

Этой областью в плоскости х₁,х₂ является четырехугольник АВСД (Рис.3.2).

Рис. 3.1. Область допустимых решений (к примеру 1).

2. Исходя из (3.9) придавая различные постоянные значения  функции

F =(X₁ – 3)² + (X₂ – 4)² = d строим линии уровня (окружности с центром в точке X₁ = 3, X₂ = 4 и радиусом R = (d)² ) для различных значений d (Рис. 3.2).

3. Находим линию уровня, которая имеет максимальное значение d, т. е. окружность максимального радиуса, проходящую через точку С. Координаты точки С, как точки пересечения прямых (3.10) и (3.12), находим решая систему уравнений (3.10), (3.12): С(13,7; 8,6).    

4. Подставляем координаты точки С в (3.9) и вычисляем максимальное значения целевой функции F_max = 135,7. Минимальное значение целевой функции F_min = 0 достигается в центре окружности. (Рис. 3.2).

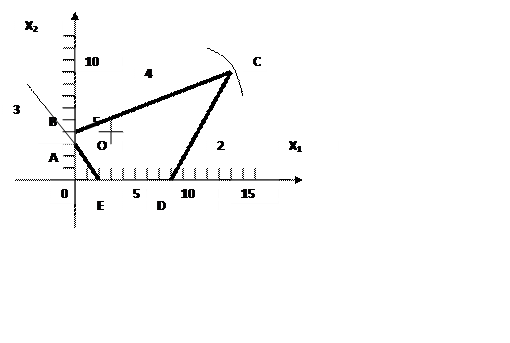
Рис. 3.2. Область допустимых решений (к примеру 2).

Пример 3.Найти максимальное и минимальное значение функции

                                       F =  (X₁ – 3)² + (X₂ – 4)²          (3,14)

при условиях:                   3 X₁ +  3 X₂ ≥ 10;            (3.15)

                                           5 X₁ +  2 X₂ ≤ 14;            (3.16)

                                         - 3 X₁ + 3 X₂ ≤ 10;             (3.17)

                                                    X₁ ,X₂ ≥ 0               (3.18)

Решение. Задача (3.14)…(3.18)  является задачей нелинейного программирования, так как целевая функция (3.14) является нелинейной.

1. Выделяем область допустимых решений задачи. . Строим прямые, определяя точки пересечения с осями координат:

3 X₁ +  3 X₂ ≥ 10; →  [(х₁=0; х₂ = 3,3); (х₁= 3,3; х₂=0)]

5 X₁ +  2 X₂ ≤ 14; → [(х₁=0; х₂=7); (х₁= 2; х₂=2,8)]

- 3 X₁ + 3 X₂ ≤ 10;   → [(х₁=0;, х₂= 3,3); (х₁= - 3,3; х₂=0)]

Этой областью в плоскости х₁,х₂ является треугольник АВС (Рис.3.3).

2. Исходя из (3.14) придавая различные постоянные значения  функции

F =(X₁ – 4)² + (X₂ – 5)² = d строим линии уровня (окружности с центром в точке X₁ = 4, X₂ = 5 и R = (d)^1/2 ) для различных значений d (Рис. 3.3).