3. Находим линию уровня, которая имеет максимальное значение d, т. е. окружность максимального радиуса, проходящую через точку А, принадлежащую области допустимых значений. Координаты точки А, как точки пересечения прямых (3.15) и (3.16) находим решая систему уравнений (3.15), (3.16): А (8/9; 22/9).
Находим линию уровня, которая имеет минимальное значение d, т. е. окружность минимального радиуса, проходящую через точку N, принадлежащую области допустимых значений, в которой окружность касается области АВС. Для нахождения координат точки N приравняем угловые коэффициенты прямой (3.15) и касательной к окружности в точке N. Из уравнения (3.15) в виде X2 = - 2,5 + 7 получим угловой коэффициент, равный -2,5. Угловой коэффициент касательной к окружности в точке N можно получить как значение производной функции X2 по переменной X1 в этой точке. Рассматривая X2 как неявную функцию X1 и дифференцируя уравнение окружности, получим:
2(X1 – 4) + 2(X2 -5) (X2)I = 0; (X2)I = - (X1 – 4)/ (X2 – 5)
Из равенства угловых коэффициентов получим одно из уравнений для определения координат точки N. Присоединяя к нему уравнение прямой (3.15), получим систему уравнений:
X1 - 2,5 X2 = - 8,5; 5 X1 + 2 X2 = 14.
Её решение дает координаты точки N: X1 =4,3; X2 = 1,2.
4. Подставляем координаты точки А в (3.14) и вычисляем максимальное значения целевой функции Fmax = 19,3. Минимальное значение целевой функции Fmin = 16,2 достигается в точке N и вычисляется путем подстановки её координат в целевую функцию (1). (Рис. 3.3).
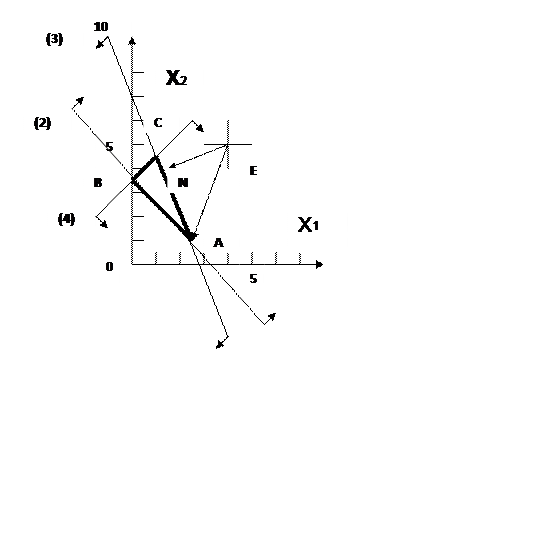
Рис.3.3. Область допустимых решений (к примеру 3)
3.2. Метод множителей Лагранжа
Рассмотрим частный случай общей задачи нелинейного программирования, предполагая что система ограничений содержит только уравнения и отсутствуют условия неотрицательности переменных, а нелинейные функции в ограничениях задачи непрерывны вместе со своими частными производными:
f(х1 , х2 , …., хn)→max (min) (3.19)
gi(х1 , х2 , …., хn) = bi (i = 1,2, m) (3.20)
Задача (3.19), (3.20) называется задачей на условный экстремум или классической задачей оптимизации.
Для нахождения решения данной задачи введем переменные גi (i = 1,2, m), называемые множителями Лагранжа и составим функцию Лагранжа:
F(х1, х2,… хn, ג1, ג2,… גm) =
f(х1
, х2 , …., хn) +
גi[bi - gi(х1
, х2 ,...,хn)] (3)
Определим частные производные 
(j = 1,2, ,n) и 
(i = 1,2, ,m) и рассматривают систему
n+m уравнений (3.22), (3.23):
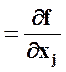
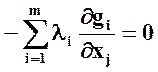(j = 1,2,…,n)
(3.22)
= bi - gi(х1
, х2 ,...,хn ) = 0 (i = 1, 2,…,m) (3.23)
c n+m неизвестными
х1 , х2 ,...,хn , ג1, ג2,… גm .
Любое решение системы (3.22),(3.23) определяет точку Х=( х10, х20 ,...,хn0) в которой может иметь место экстремум функции f(х1 , х2 , …., хn). Решив эту систему уравнений получим все точки, в которых функция (3.19) может иметь экстремальное значение. Далее проводится исследование стационарных точек как и в случае безусловного экстремума.
Последовательность определения экстремальных точек в задаче (3.19), (3.20) методом множителей Лагранжа можно представить в виде:
1. Составляем функцию Лагранжа.
2. Находим частные производные от функции Лагранжа по переменным хj, גi и приравниваем их нулю.
3. Решаем систему уравнений (3.22), (3.23) и находим точки, в которых целевая функция задачи может иметь экстремум.
4. Среди найденных точек находим такие точки, в которых достигается экстремум и вычисляем значение функции в этих точках.
Пример Предприятие изготавливает 151 изделие по двум различным технологиям. При изготовлении х1 изделий по первой технологии затраты составляют 2х1 + (х1)2 руб., а при изготовлении по второй технологии х2 изделий затраты составляют 4 х2 + (х2)2. Определить при каком количестве изделий х1 и х2 изготовленных по первой и по второй технологиям затраты на производство изделий минимальны.
Решение. Целевая функция задачи имеет вид:
f = 2 х1 + (х1)2 + 4 х2 + (х2)2 (3.24)
при условиях
х1 + х2 = 151 (3.25)
х1, х2 ≥ 0 (3.26)
Найдем минимум целевой функции без учета условия неотрицательности переменных. Составим функцию Лагранжа:
F(х1, х2, ג1) = 2 х1 + (х1)2 + 4 х2 + (х2)2 + ג[151-х1 -х2 ]
Находим частные производные по х1, х2, ג и приравниваем их нулю:
= 2 +2 х1 - ג = 0
= 4 + 2 х1 - ג = 0
= 151 - х1 - х2
= 0
Исключая из первых двух уравнений ג получим 4х1 +2 х2 = 2 + 2 х1, или х1 - х2 = 1. Решая это уравнение совместно с уравнением х1 - х2 = 151 находим х1* = 76,0; х2* = 75,0. Эти значения удовлетворяют условиям (3.26) неотрицательности переменных. Точка с координатами х1*, х2* является подозрительной на экстремум. Определяя вторые производные от функции f в точке х1* х2* найдем, что в этой точке имеет место условный минимум:
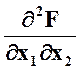= 0;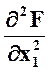 
= 2 > 0; 
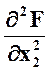= 2; ∆ = 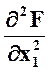. 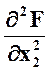- 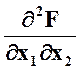= 4 > 0.
f = 2.76,0 + (76,0)2 + 4.75,0 + (75,0)2 = 11853.
Т. о. затраты будут минимальными, если предприятие изготовит 76 изделий по первой технологии, и 75 изделий по технологии второго вида.
3.3. Другие методы решения задач нелинейного программирования с ограничениями.
Для изучения данной темы следует обратиться к [6] c. 258…303; [4] с. 108…144.
Вопросы для самоконтроля
1. В каких случаях задача математического программирования является нелинейной?
2. В чем заключается геометрическая интерпретация задачи нелинейного программирования?
3. Как определяется область допустимых решений в случае решения задачи нелинейного программирования на основе ее геометрической интерпретации?
4. Что такое поверхность уровня?
5. Как определяется оптимальное решение в случае решения задачи нелинейного программирования на основе ее геометрической интерпретации?
6. В чем заключается метод множителей Лагранжа?
7. Что такое функция Лагранжа?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.