Прохождение света через сферическую границу раздела, страница 5

T = 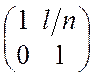,                                                                                                (2.18)

где L = l /n –приведенная длина оптического промежутка:

.

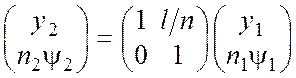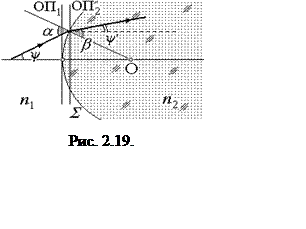Для нахождения матрицы преломления выберем опорные плоскости ОП₁ и ОП₂ в непосредственной близости от преломляющей поверхности по обе ее стороны (рис. 2.19). Расстояние между ними в параксиальном приближении пренебрежимо мало, поэтому можно считать, что луч пересекает обе плоскости на одной высоте: y₂ = y₁. Для параметра ny из несложных геометрических преобразований с учетом закона преломления получаем ny₂ = ny₁ –Dy₁, где D – оптическая сила преломляющей поверхности , см. формулу 2.3. Таким образом, матрица преломления имеет вид

R = 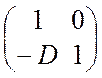,  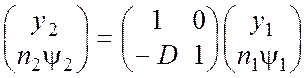         .                     (2.19)

Правило знаков позволяет распространить формулу (2.19) и на сферические зеркала, заменив n₂ на (–n₁) и использовав для оптической силы выражение (2.6).

Если произвольная оптическая система состоит из N элементов (оптических промежутков и преломляющих поверхностей), то каждый из них описывается своей матрицей преобразования M_m. Обозначив вектор луча  на
m-й опорной плоскости, находящейся перед соответствующим элементом через K_m, получим рекуррентное соотношение: K_m+1 = M_m×K_m, аналогично
K_m = M_m-1×K_m-1 и т. д. Отсюда находим, что для опорной плоскости ОП_N+1, находящейся на выходе из системы, K_N+1 = M×K₁, где M×– матрица преобразования системы, представляющая собой произведение всех матриц, взятых в обратном порядке:

M = M_N×M_N-1×M_N-2×…×M₁.                                                                                 (2.20)

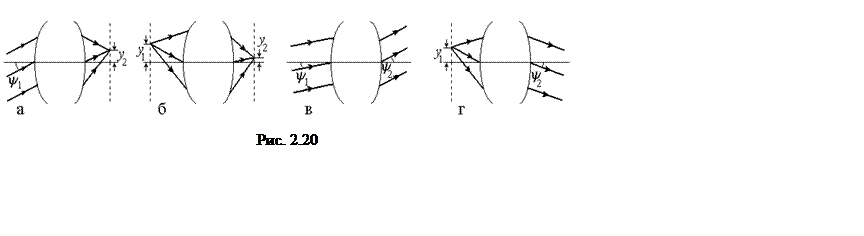
Так например, для толстой линзы в воздухе, представляющей собой однородную среду толщиной l с показателем преломления n (стекло), ограниченную сферическими поверхностями с радиусами кривизны R₁ и R₂, получаем:

.

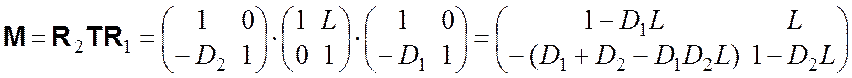Как и следовало ожидать, оптическая сила такой линзы не равна сумме оптических сил составляющих ее поверхностей, а определяется как . В частном случае тонкой линзы L®0, матрица T вырождается в единичную и общая матрица преобразования M имеет такой же вид, как матрица R преломления на одной поверхности, но с оптической силой D = D₁+D₂.

Отметим, что определители матриц T и R равны единице :AD – BC = 1. Следовательно, будет равен единице и определитель матрицы для любой оптической системы. Для того, чтобы лучше представить смысл элементов матрицы преобразования A, B, C и D, рассмотрим, в каких случаях один из элементов обращается в нуль.

- 

A = 0, следовательно y₂ = B×n₁y₁. Это значит, что все лучи, входящие в систему под одинаковым углом, пройдут через одну и ту же точку на выходной плоскости ОП₂ (рис. 2.20а). Следовательно, ОП₂ является задней фокальной плоскостью системы.

-  B = 0, следовательно y₂ = A×y₁. Все лучи, выходящие из точки S с координатой y₁ на плоскости ОП₁, попадут в точку P с координатой y₂ на плоскости ОП₂ (рис. 2.20б). Таким образом, точки S и P являются объектом и изображением, а плоскости ОП₁ и ОП₂ – сопряженными плоскостями. Величина A = y₂ / y₁ дает увеличение системы.

-  C = 0, тогда n₂y₂ = D×n₁y₁. В этом случае все лучи, входящие в систему параллельно друг другу под углом y₁ к оптической оси, на выходе дадут также параллельный пучок (рис. 2.20в). Оптическая система, преобразующая параллельный пучок лучей в параллельный же, называется афокальной или телескопической. Величина y₂ /y₁ = n₁×D /n₂ представляет собой угловое увеличение системы.

-  D = 0, при этом n₂y₂ = C×y₁. Все лучи, выходящие из точки y₁ входной опорной плоскости, выйдут из системы под одинаковым углом (рис. 2.20г). Следовательно, ОП₁ – передняя фокальная плоскость системы.

-  Если один из элементов A или D равен нулю, то условие AD – BC = 1 требует, чтобы BC = –1. Аналогично, если в нуль обращается B или C, то AD = 1.

1.5  Глаз как оптическая система.

Не вдаваясь в строение глаза и физиологию зрения, рассмотрим, как работает оптическая система глаза – хрусталик. Хрусталик представляет собой прозрачное бесцветное тело, напоминающее двояковыпуклую линзу, передняя поверхность которой менее выпуклая, чем задняя. Он состоит из слоев различной плотности, имеющих волокнистое строение. Мышца глаза, рефлекторно напрягаясь или расслабляясь, может менять кривизну поверхностей хрусталика, главным образом, передней. Таким образом осуществляется аккомодация, т. е. изменение оптической силы глаза, позволяющее фокусировать изображение на сетчатке. Так как деформация хрусталика может происходить только в определенных пределах, то для всякого глаза существуют определенные границы, в пределах которых глаз может отчетливо видеть предметы. Эти границы определяют так называемую область аккомодации глаза. Наиболее отдаленная граница, которую глаз может отчетливо видеть при ненапряженной мышце, называется дальней, а ближайшая граница, которую он способен отчетливо видеть при максимальном напряжении мышцы, - ближней точкой ясного видения. В ненапряженном состоянии нормальный глаз аккомодирован на рассмотрение бесконечно удаленных предметов, т. е. он собирает параллельные лучи в точке сетчатки (рис. 2.21а). Таким образом дальняя точка ясного видения для нормального глаза находится в бесконечности. В возрасте до десяти лет ближняя точка нормального глаза лежит на расстоянии 7…8 см от глаза. К тридцати годам это расстояние увеличивается примерно до 15 см.

При приближении рассматриваемого предмета к глазу увеличивается угол зрения, а с ним и размеры изображения на сетчатке. Это позволяет рассмотреть более мелкие детали. Однако при максимально возможном приближении усиливается напряжение мышцы, деформирующей хрусталик, работа глаза становится утомительной. В случае нормального глаза оптимальное расстояние для чтения и письма составляет около 25 см. Это расстояние для нормального глаза и принимается условно за расстояние наилучшего видения.

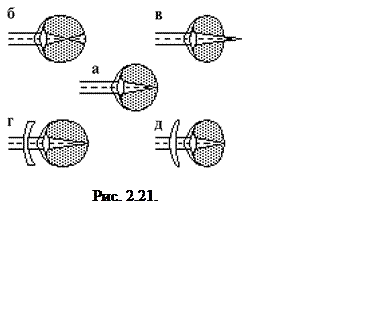У близорукого глаза (рис. 2.21б) оба предела наилучшего видения находятся ближе, а ближний предел дальнозоркого глаза - дальше, чем у нормального глаза. Дальний предел дальнозоркого глаза всегда отрицателен, т. е. дальняя точка ясного видения находится не спереди, а позади глаза (рис. 2.21в). Такой глаз в ненапряженном состоянии может собирать на сетчатке только сходящиеся пучки лучей. У близорукого глаза в ненапряженном состоянии параллельные лучи сходятся перед, а у дальнозоркого - за сетчаткой.