Прохождение света через сферическую границу раздела, страница 3

1.2  Преломление света в линзе. Формула тонкой линзы

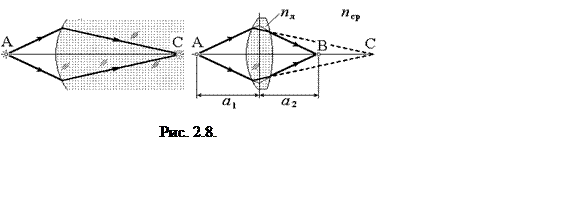
Простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, отделяющих какой-либо прозрачный, хорошо преломляющий материал от окружающей среды, имеет очень большое значение. Такая система представляет собой линзу и играет важную роль во многих оптических приборах.

Линза называется тонкой, если расстояние между вершинами сферических поверхностей, ограничивающих ее, мало по сравнению с радиусами кривизны поверхностей. Для тонкой линзы можно считать вершины преломляющих поверхностей совпадающими в одной точке, которая носит название оптического центра линзы. Любой параксиальный луч, проходящий через точку оптического центра, практически не испытывает преломления. Действительно, для таких лучей участки обеих поверхностей линзы можно считать параллельными, так что луч, проходя через них, не меняет направления, но лишь смещается параллельно самому себе (преломление в плоскопараллельной пластинке), а так как толщиной линзы можно пренебречь, то смещение это ничтожно и луч практически проходит без преломления. Луч, проходящий через центр, называется осью линзы. Та из осей, которая проходит через центры кривизны обеих поверхностей, называется главной, остальные - побочными.

Выражение, связывающее положение предмета и его изображения в линзе (формула линзы) может быть выведена, если рассматривать два последовательных преломления лучей на каждой из границ раздела (рис. 2.8). Первая (по ходу луча) преломляющая поверхность дает изображение предмета А в точке С, которое, в свою очередь, является предметом для второй по ходу луча поверхности. Окончательное изображение предмета А в линзе - точка В. Представленное ниже выражение было получено при тех же ограничениях, которые мы ввели при преломлении на одной сферической границе раздела сред. Условия: гомоцентричность пучков, стигматичность изображений, параксиальность и правило знаков. Главные плоскости тонкой линзы совпадают и проходят перпендикулярно главной оптической оси в оптическом центре, поэтому расстояния от предмета и изображения отсчитываются от оптического центра линзы (а₁ и а₂). Показатель преломления линзы обозначим n_л, показатель преломления однородной среды, в которой (будем считать) находится линза – n_ср. R₁ – радиус кривизны первой по ходу луча сферической преломляющей поверхности, R₂ радиус второй. В этом случае формула линзы будет иметь вид:

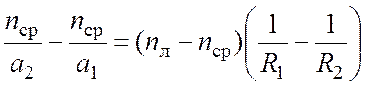                                                 (2.12)

Выражение позволяет однозначно определить положение изображения, если задано положение предмета. Правая часть равенства не зависит от положения предмета и его изображения и определяется только свойствами самой оптической системы. Первая скобка (n_л – n_ср) определяет физические параметры системы, а (1/R₁ – 1/R₂) – геометрические. По аналогии с формулой сферической преломляющей поверхности, правая часть выражения (2.12) названа оптической силой тонкой линзы:

.                                               (2.13)

Легко показать, что оптическая сила тонкой линзы по сути есть сумма оптических сил ее поверхностей. Действительно:

Измеряется оптическая сила линзы в диоптриях (дптр). 1 дптр - это оптическая сила линзы, находящейся в воздухе, имеющей фокусное расстояние в 1 метр.

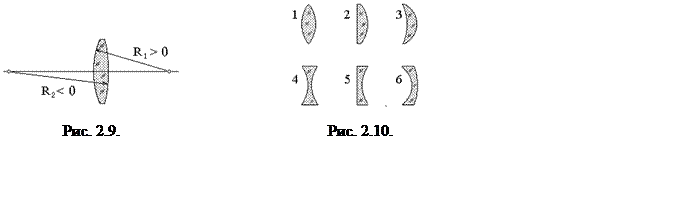
Линза называется собирающей (положительной), если D > 0; рассеивающей (отрицательной), если D < 0. В случае линзы представленной на рис. 2.9: R₁ > 0, а R₂ < 0, тогда  и оптическая сила такой линзы D > 0, если n_л > n_ср. Таким образом, знак оптической силы линзы определяется ее геометрическими параметрами и соотношением показателей преломления сред.

На рис. 2.10 представлены линзы различной конфигурации. Если n_л > n_ср, то линзы под номерами 1, 2, 3 являются положительными, а под номерами 4, 5, 6 - отрицательными, если же n_л < n_ср, то наоборот.

Рассматривая тонкую линзу, находящуюся в однородной среде, можно ввести величины

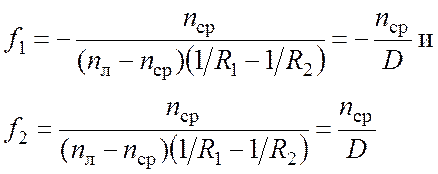,                                  (2.14)

определяющие положения точек главных фокусов этой оптической системы. Они получены по аналогии с фокусными расстояниями сферической преломляющей поверхности и, как видно, имеют разные знаки. Таким образом, точки фокусов лежат по разные стороны от линзы (точка первого фокуса - перед линзой, точка второго фокуса - за линзой по ходу луча), но равны по абсолютной величине. Поэтому иногда, используя физический жаргон, говорят о «фокусе» линзы (одном фокусном расстоянии).

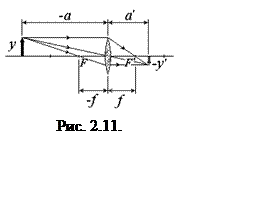
Пример построения изображения в тонкой линзе представлен на рис. 2.11. Здесь собирающая (положительная) линза строит действительное, перевернутое и уменьшенное изображение y¢ предмета y. Линейное (поперечное) увеличение, даваемое тонкой линзой, рассчитывается точно так же, как и для одной поверхности:

.                                                       (2.15)

Аналогично вышеизложенному, найдем, что для перевернутых действительных изображений увеличение отрицательно, а для прямых мнимых V > 0.

Величина и знак линейного увеличения для одной и той же линзы зависят от расположения предмета. Если предмет расположен за двойным фокусом собирающей линзы (рис. 2.12а), то его изображение оказывается действительным, перевернутым и уменьшенным.

Если предмет находится в точке двойного фокуса, то изображение становится равным, оставаясь действительным и перевернутым (рис. 2.12б). При дальнейшем приближении предмета к линзе изображение постепенно отдаляется, увеличиваясь в размерах, а при достижении предметом передней фокальной плоскости – переносится в бесконечность (рис. 2.12в, г).

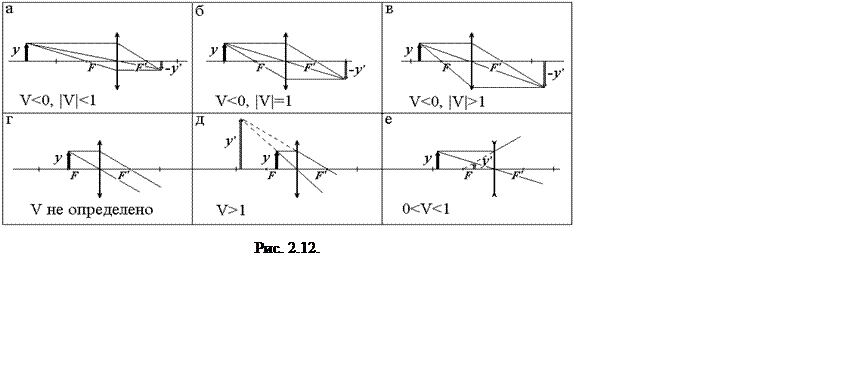Расположение предмета между фокусом и линзой приводит к формированию мнимого, прямого, увеличенного изображения (случай увеличительного стекла или лупы, рис. 2.12д).

Отрицательная (рассеивающая) линза характеризуется существенно меньшей вариативностью формируемых изображений: при любом расположении предмета изображение получается мнимым, прямым и уменьшенным (рис. 2.12е).

Если есть оптическая система, состоящая из нескольких сложенных вместе тонких линз, находящихся в однородной среде (n_ср), то для определения фокусного расстояния такой системы можно воспользоваться выражением

,                                                                      (2.16)

где D_сист определяется как сумма оптических сил каждой линзы в отдельности, рассчитанных для той среды, в которой находится сама система.