Прохождение света через сферическую границу раздела, страница 2

Очевидно, что для сферического зеркала .

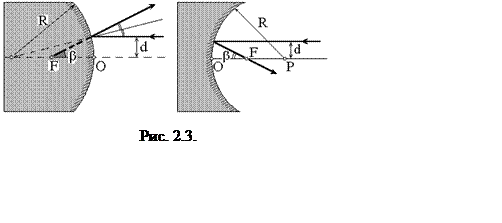
Случаи вогнутого и выпуклого зеркала отличаются лишь знаком R. Легко видеть, что фокус вогнутого зеркала - действительный, а фокус выпуклого зеркала - мнимый (рис. 2.3).

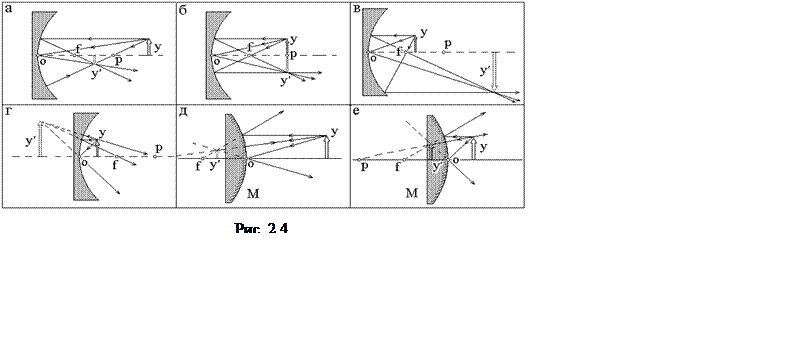
Примеры построения изображений в зеркалах приведены на рис. 2.4 а–е. Во всех случаях использованы те лучи, ход которых легко определить. Для вогнутого зеркала луч, идущий параллельно оптической оси, после отражения проходит через фокус зеркала; луч, прошедший через фокус, отражается параллельно оптической оси; луч, попавший в вершину зеркала, отражается под тем же углом к оптической оси; луч, прошедший через центр кривизны, отражается обратно. Аналогично выполняется построение для выпуклого зеркала, но в этом случае через фокус или центр кривизны проходят продолжения лучей.

Плоское зеркало может рассматриваться как частный случай сферического зеркала. У плоской поверхности радиус кривизны , и оптическая сила D = 0, а по формуле сферической преломляющей поверхности (2.2), учитывая, что n₂ = - n₁, получим: a₂ = – a_1. Это еще раз подтверждает сделанный ранее вывод: изображение предмета в плоском зеркале мнимое, равное и симметрично расположенное.

Линейные и угловые характеристики изображений

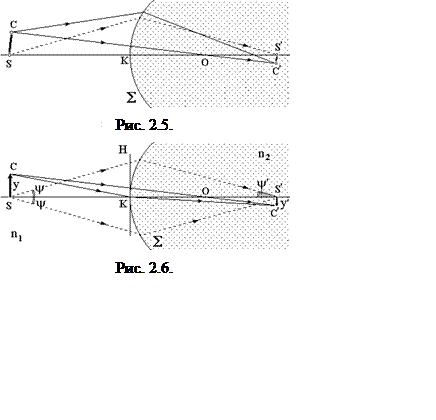Построим изображение маленькой части сферы SC , полученное при прохождении лучей через границу раздела. Отметим точку S¢, сопряженную точке S, и точку C¢ сопряженную точке С (рис. 2.5). Если отрезки SC и S¢C¢ очень малы, то вместо самих дуг, как элементов сферы, в расчет можно брать аппроксимирующие их хорды (элементы плоскости).

Используя свойства параксиальных гомоцентрических пучков, можно построить изображение небольших протяженных предметов при преломлении на сферической поверхности. Плоскость предмета SC и плоскость его изображения S¢C¢ называются плоскостями, сопряженными по отношению к данной оптической системе.

Поставив предмет SC перпендикулярно главной оптической оси, получим изображение S¢C¢ (рис. 2.6). Обозначим длину отрезка SC через y, отрезка S¢C¢ – через y¢. Отношение размера изображения к размеру предмета носит название линейного или поперечного увеличения:

.                                                                              (2.7)

Приписывая SC и S¢C¢ знаки (как обычно), получим, что увеличение положительно, если изображение прямое, и отрицательно, если изображение перевернутое.

Для малых SC и S¢C¢ находим:

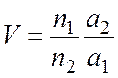.                                                                                                    (2.8)

У преломляющей системы показатели преломления n₁ и n₂ всегда положительны, так что знак увеличения определится знаком отношения а₂ /а₁. Для расположения изображения и предмета, соответствующего рис. 2.6, отрезки а₁ и а₂ имеют разные знаки, т. е. V отрицательно, а изображение перевернутое; для мнимых изображений - наоборот.

Сопряженные плоскости называются главными, если для них V = 1, т. е. изображение получается прямым и в натуральную величину объекта. Оптическая система из одной преломляющей поверхности представляет собой вырожденный случай: главные плоскости совпадают между собой и представлены плоскостью H, касательной к сфере в точке K (рис. 2.6), т. е. а₁ = а₂ = 0. Соответственно и фокусные расстояния сферической поверхности следует считать расстояниями от этой единственной главной плоскости до фокусов.

Углы y и y¢ на рис. 2.6 определяют максимальное раскрытие (апертуру) пучков, падающих на поверхность å (угол 2y), и сопряженных им изображающих пучков (угол 2y¢). Предельное значение этих углов определяется требованием соблюдения условий параксиальности. При выполнении условий параксиальности без искажения передается изображение не только точки, но и небольшого предмета, расположенного около оси оптической системы. Оправа линзы или другое отверстие, ограничивающее углы y и y¢, называется апертурной диафрагмой.

Для параксиальных лучей имеет место соотношение

,                                                                                          (2.9)

носящее название теоремы Лагранжа-Гельмгольца.

При использовании пучков со значительной апертурой получение четких изображений возможно лишь при выполнении условия

                                                                         (2.10)

(условие синусов Аббе). Для параксиальных лучей углы y и y¢ малы, так что условие Аббе переходит в уравнение (2.9).

Условие Лагранжа-Гельмгольца или условие синусов налагает ограничение на свободу преобразования световых пучков при помощи оптических систем, связывая апертуру и размер предмета с апертурой и размером изображения. Из него вытекает, что преобразование данного оптического пучка при помощи оптической системы в другой пучок любого, наперед заданного строения невозможно. Строение преобразованного пучка может быть только таким, какое допускает условие Лагранжа-Гельмгольца.

Это важное принципиальное ограничение приобретает особое значение в вопросах фотометрии и концентрирования лучистой энергии при помощи оптических систем.

Центрированная оптическая система

Преломление на одной сферической границе раздела двух сред используется сравнительно редко. Большинство реальных преломляющих систем содержит, по крайней мере, две преломляющие поверхности (линза), или большее их количество.

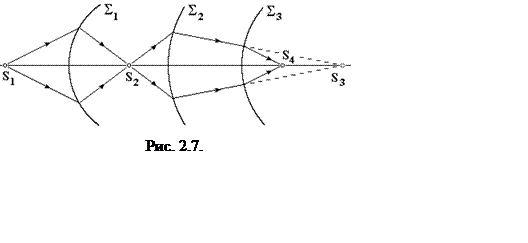Система сферических поверхностей называется центрированной, если центры всех поверхностей лежат на одной прямой, которая называется главной оптической осью системы (рис. 2.7).

В центрированной оптической системе при произвольном числе преломлений на границах раздела гомоцентрический параксиальный пучок остается гомоцентрическим и дает стигматическое изображение.

Изображение малых отрезков происходит аналогично тому, как это происходит на одной преломляющей поверхности. В центрированной системе имеет место наличие двух фокусов и двух фокальных плоскостей установленное для одной поверхности, а также сохраняет силу теорема Лагранжа-Гельмгольца:

                                                  (2.11)

Для центрированной оптической системы сохраняет смысл и понятие главных плоскостей, как таких сопряженных плоскостей, в которых объект и изображение имеют одинаковые величину и направление. Но в то же время если для одной преломляющей сферической поверхности обе главные плоскости сливались в одну, касающуюся ее вершины, то для центрированной системы эти две плоскости уже не совпадают. Фокусные расстояния системы, так же как в случае одной сферической поверхности рассчитываются как расстояния от соответствующей главной плоскости до фокуса.