Сформулированные выше законы поведения света носят общий характер. Полезно для упрощения решения практических задач рассмотреть поведение света и построение изображений на неплоских, в частности, сферических границах раздела.
 Пусть
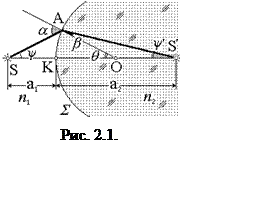
свет от точечного источника S падает на сферическую границу раздела двух
сред S с показателями преломления n1
и n2, где n2 > n1
(рис. 2.1). Индексация определяет порядок прохождения сред, (луч падает на
границу раздела из первой среды и проходит во вторую). Ход лучей через эту
границу построен по общим законам геометрической оптики. Изображение S¢ получено как точка пересечения двух лучей исходящих из точки
предмета S. Линия SS´, по которой идет луч, проходящий границу
раздела S по перпендикуляру, носит название главной
оптической оси системы. Точка K – вершина поверхности S, точка О – центр кривизны этой поверхности.
Пусть
свет от точечного источника S падает на сферическую границу раздела двух
сред S с показателями преломления n1
и n2, где n2 > n1
(рис. 2.1). Индексация определяет порядок прохождения сред, (луч падает на
границу раздела из первой среды и проходит во вторую). Ход лучей через эту
границу построен по общим законам геометрической оптики. Изображение S¢ получено как точка пересечения двух лучей исходящих из точки
предмета S. Линия SS´, по которой идет луч, проходящий границу
раздела S по перпендикуляру, носит название главной
оптической оси системы. Точка K – вершина поверхности S, точка О – центр кривизны этой поверхности.
Уточним условия (или ограничения), при которых рассматривается преломление света на сферической границе раздела.
а) пучки гомоцентрические;
б) изображения стигматические;
в) пучки параксиальные – это означает, что углы y и y´ малы, так, что можно считать равными отрезки SK @ SA и AS´ @ KS´.
Без этих условий мы не получим четких изображений, будут иметься искажения или аберрации, речь о которых пойдет далее (см. раздел 2.6).
При выводе выражения, связывающего положения изображения и самой точки предмета, будем пользоваться правилом знаков: поставив предмет по одну сторону преломляющей поверхности, выбираем направление хода лучей через систему. Отсчет отрезков (расстояние от предмета до границы раздела, расстояние до изображения от границы раздела, радиус кривизны границы раздела) производится от преломляющей поверхности в сторону окончания отрезка. Если направление отсчета совпадает с направлением хода луча через систему, то такой отрезок считается положительным, если направление отсчета противоположно ходу луча через систему – такой отрезок отрицателен. Показатели преломления сред, разделенных преломляющей поверхностью, тоже имеют знаки. Если после границы раздела луч продолжает идти в том же направлении, то для него и первая среда и вторая имеют положительные показатели преломления. Для рисунка 2.1 показатели преломления сред положительны. Если лучи проходят систему против выбранного направления (например, отражаются), то для них показателям преломления соответствующих сред приписываются отрицательные значения.
Учитывая условия (а-в) и правило знаков, обозначим SK @ SA = - а1, AS´ @ KS´ = а2 и AO @ KO = R (радиус сферической поверхности). Написав закон преломления на границе раздела, и решая задачу геометрически, получим выражение:
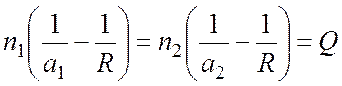 . (2.1)
. (2.1)
Последнее выражение показывает, что
произведение 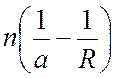 при преломлении сохраняет
свою величину Q. Его называют инвариантом Аббе. Для расчетов
этот инвариант удобнее записать в виде
при преломлении сохраняет
свою величину Q. Его называют инвариантом Аббе. Для расчетов
этот инвариант удобнее записать в виде
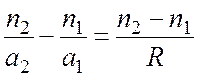 . (2.2)
. (2.2)
Это выражение носит название формула сферической преломляющей поверхности. Она позволяет однозначно определить положение изображения, если известно положение предмета и наоборот. Правая часть этого равенства не зависит от положения предмета и его изображения, а определяется только свойствами самой оптической системы, и носит название оптическая сила (D) сферической преломляющей поверхности.
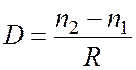 (2.3)
(2.3)
Пользуясь установленным выше правилом знаков, можно выяснить, какие изображения получаются в случае выпуклой (R>0) и вогнутой (R<0) поверхностей. Точно так же в зависимости от того, будут ли а1 и а2 иметь разные знаки или одинаковые, мы будем иметь случаи, когда изображение располагается с противоположной по сравнению с источником стороны преломляющей поверхности или лежит по одну сторону ним. В первом случае (а2 > 0) точка, именуемая изображением, есть действительно точка пересечения преломленных лучей. Такое изображение называется действительным (см. рис. 2.1). Во втором случае (а2 < 0), очевидно, преломленные лучи, идущие во второй среде, остаются расходящимися и реально не пересекаются. В этом случае название изображения относится к той воображаемой точке, которая представляет собой место пересечения предполагаемого продолжения преломленных лучей. Такое изображение называется мнимым.
 Помимо
оптической силы сферической преломляющей поверхности данную оптическую систему
характеризуют постоянные величины называемые фокусными расстояниями.
Точкой переднего фокуса F по определению называется точка
на оптической оси, в которую надо поместить предмет, чтобы после преломления на
сферической преломляющей поверхности изображение находилось на бесконечности
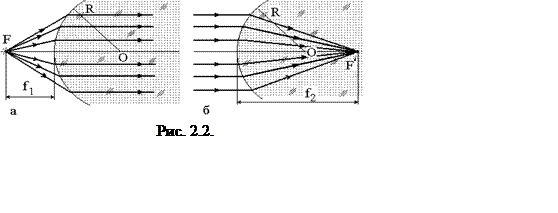
(рис. 2.2а). Расстояние f1 от поверхности å до точки первого фокуса называется передним фокусным расстоянием
и определяется из выражения (2.2) при условии а2 = ¥ как:
Помимо
оптической силы сферической преломляющей поверхности данную оптическую систему
характеризуют постоянные величины называемые фокусными расстояниями.
Точкой переднего фокуса F по определению называется точка
на оптической оси, в которую надо поместить предмет, чтобы после преломления на
сферической преломляющей поверхности изображение находилось на бесконечности
(рис. 2.2а). Расстояние f1 от поверхности å до точки первого фокуса называется передним фокусным расстоянием
и определяется из выражения (2.2) при условии а2 = ¥ как:
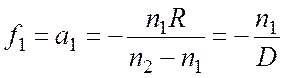 . (2.4)
. (2.4)
Точкой заднего фокуса F’ по определению называется точка на оптической оси, куда после преломления на сферической преломляющей поверхности соберутся лучи от предмета, находящегося на бесконечности (рис. 2.2б). Расстояние f2 от поверхности å до точки заднего фокуса называется задним фокусным расстоянием и определяется из выражения (2.2) при условии а1 = ¥:
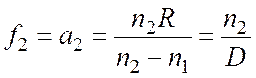 . (2.5)
. (2.5)
В данном случае . точки
фокусов лежат по разные стороны сферической границы раздела и, в соответствии с
правилом знаков, переднее фокусное расстояние отрицательно, а заднее –
положительно. Как видно, ![]() ,
т. е соответствующие фокусные расстояния прямо пропорциональны показателям
преломления сред, в которых они расположены.
,
т. е соответствующие фокусные расстояния прямо пропорциональны показателям
преломления сред, в которых они расположены.
Практическим важным случаем является отражение света от сферического зеркала. Например: если границу раздела на рисунке 2.2 сделать зеркальной (это будет выпуклое сферическое зеркало), то при попадании луча на границу раздела, зеркало отражает луч обратно в среду с показателем преломления n1. Для луча отраженного показатель преломления второй среды n2 = - n1 и выражение (2.3) будет иметь вид:
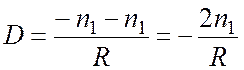 . (2.6)
. (2.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.