 На
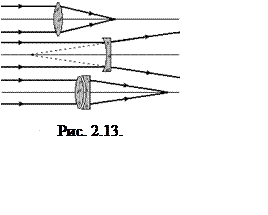
рис. 2.13 изображена система двух линз, собирающей и рассеивающей. Видно,
что оптическая сила собирающей линзы по модулю больше, чем рассеивающей (ее
фокусное расстояние короче). Поэтому при их совмещении друг с другом итоговая
оптическая сила оказывается положительной: D = D1+D2 >0.Естественно,
что оптическая сила такой системы меньше, чем у первой (собирающей) линзы, а
фокусное расстояние – больше.
На
рис. 2.13 изображена система двух линз, собирающей и рассеивающей. Видно,
что оптическая сила собирающей линзы по модулю больше, чем рассеивающей (ее
фокусное расстояние короче). Поэтому при их совмещении друг с другом итоговая
оптическая сила оказывается положительной: D = D1+D2 >0.Естественно,
что оптическая сила такой системы меньше, чем у первой (собирающей) линзы, а
фокусное расстояние – больше.
Если в многолинзовой системе оптические элементы расположены на конечных расстояниях друг от друга, то оптическая сила такой системы не равна простой сумме оптических сил составляющих ее линз, а зависит от расстояния между линзами L (см. ниже раздел 2.5):
![]() .
.
Тонкая линза как система двух центрированных поверхностей представляет собой простейшую оптическую систему, дающую довольно несовершенное изображение. В большинстве случаев мы прибегаем к построению более сложных систем, характеризующихся наличием большого числа преломляющих поверхностей и не ограниченных требованием близости этих поверхностей (тонкости линзы).
В 1841 году Гаусс дал общую теорию оптических систем, получившую дальнейшее развитие в трудах многих математиков и физиков. Теория Гаусса - теория идеальной оптической системы, т. е. системы, в которой сохраняется гомоцентричность пучков и изображение геометрически подобно предмету. Согласно этому определению всякой точке пространства объектов соответствует в идеальной системе точка пространства изображений; эти точки носят название сопряженных. Точно так же каждой прямой или плоскости пространства объектов должна соответствовать сопряженная прямая или плоскость пространства изображений. Иными словами, теория идеальной оптической системы - чисто геометрическая теория, устанавливающая соотношение между точками, линиями, плоскостями.
Изложенное в разделе 2.1 показывает, что идеальная оптическая система может быть осуществлена с достаточным приближением в виде центрированной оптической системы, если ограничиться областью вблизи оси симметрии, т. е. параксиальными пучками. В теории Гаусса требование тонкости системы отпадает, но лучи по-прежнему предполагаются параксиальными. Нахождение физической системы, которая приближалась бы к идеальной даже при пучках значительного раскрытия, есть задача прикладной геометрической оптики.
Линия, соединяющая центры кривизны сферических поверхностей, представляет собой ось симметрии центрированной системы (рис. 2.14 - ось ОО¢) и называется главной оптической осью системы. Теория Гаусса устанавливает ряд так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства оптической системы и позволяет пользоваться ею, не строя реального хода лучей в системе.
 Рассматривая,
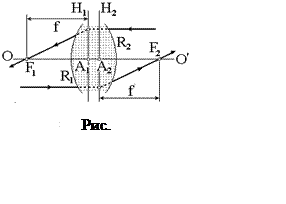
чисто геометрически, сопряженные друг другу лучи, проходящие через
центрированную оптическую систему (рис. 2.14), получим, что любой точке на
проекции плоскости Н1 найдется сопряженная точка на проекции
плоскости Н2, например, R1 и R2. К тому же А1R1
=А2R2, т. е. увеличение:
Рассматривая,
чисто геометрически, сопряженные друг другу лучи, проходящие через
центрированную оптическую систему (рис. 2.14), получим, что любой точке на
проекции плоскости Н1 найдется сопряженная точка на проекции
плоскости Н2, например, R1 и R2. К тому же А1R1
=А2R2, т. е. увеличение:
V = A2R2 / A1R1=1.
Таким образом, плоскости Н1 и Н2
перпендикулярные к главной оптической оси изображаются друг в друге прямо и в
натуральную величину и называются, как уже отмечалось в разделе 2.1, главными
плоскостями. Точки А1 и А2 пересечения главных
плоскостей с осью носят название главных точек системы.
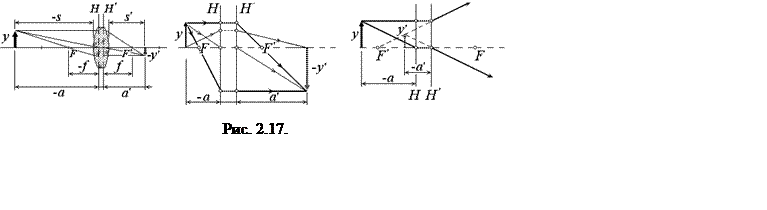
Расстояния от главных точек до фокусов называются фокусными расстояниями
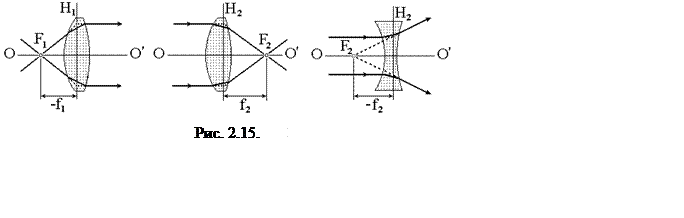
системы (на рис. 2.14 - расстояния f). На
рис. 2.15 показаны примеры определения фокусных расстояний в толстой
линзе, частном случае простейшей центрированной оптической системы.
 |
 |
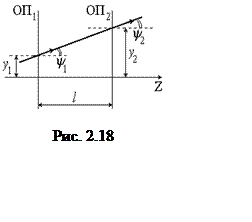 Траектория
любого луча, проходящего через оптическую систему, представленную набором
преломляющих поверхностей, состоит из отрезков прямых линий. В приближении
гауссовой оптики каждый меридиональный луч, т. е. луч,
лежащий в одной плоскости с оптической осью системы Z, можно задать двумя
параметрами. Этими параметрами являются: высота y, на которой этот луч
пересекает некоторую заранее выбранную опорную плоскость (ОП) z = const
и угол y между лучом и оптической осью (рис. 2.18). Для
проведения расчетов оказывается удобнее заменить угол y соответствующим ему параметром ny (или, точнее
говоря, n×siny).
Траектория
любого луча, проходящего через оптическую систему, представленную набором
преломляющих поверхностей, состоит из отрезков прямых линий. В приближении
гауссовой оптики каждый меридиональный луч, т. е. луч,
лежащий в одной плоскости с оптической осью системы Z, можно задать двумя
параметрами. Этими параметрами являются: высота y, на которой этот луч
пересекает некоторую заранее выбранную опорную плоскость (ОП) z = const
и угол y между лучом и оптической осью (рис. 2.18). Для
проведения расчетов оказывается удобнее заменить угол y соответствующим ему параметром ny (или, точнее
говоря, n×siny).
Для исследования поведения луча при прохождении оптической системы необходимо рассмотреть только два основных процесса:
- Перемещение между двумя преломляющими поверхностями – оптический промежуток. Луч просто проходит по прямой линии от одной поверхности к другой. Область между поверхностями характеризуется ее толщиной l и показателем преломления среды n.
- Преломление на сферической границе раздела радиуса R между областями с показателями преломления n1 и n2.
Преобразование параметров y и ny луча при переходе от одной опорной плоскости к другой в параксиальном приближении линейно и имеет вид
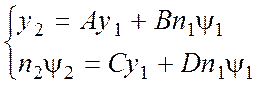 .
.
Это преобразование можно записать в матричной форме:
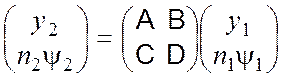 . (2.17)
. (2.17)
Таким образом, каждому элементу оптической системы можно сопоставить свою матрицу преобразования лучей. Для того, чтобы получить общую матрицу преобразования лучей, описывающую оптическую систему в целом, нужно просто перемножить в правильной последовательности все матрицы перемещений, преломлений и отражений, встречающиеся в системе.
Очевидно, что при прохождении луча через оптический промежуток угол наклона y остается постоянным, а высота изменяется по закону y2 = y1+ tgy (рис. 2.18). Переходя от угла наклона к параметру ny и учитывая, что в параксиальном приближении tgy » y, находим, что преобразование параметров луча оптическим промежутком можно описать матрицей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.