Преобразование программной информации, интерполяторы. Схемы использования интерполяторов, страница 7

КРУГОВАЯ ИНТЕРПОЛЯЦИЯ 

ПО МЕТОДУ ОЦЕНОЧНОЙ ФУНКЦИИ

Применение метода оценочной функции при круговой интерполяции осуществляется в том же порядке, что и при линейной интерполяции. Уравнение окружности запишем в форме

                                                    xi2 + yi2 = R2.

Оценочной функцией F_i для окружности является выражение

                                                Fi = xi2 + yi2 − R2, где x_i, y_i – текущие значения координат траектории; R – радиус окружности.

Знак оценочной функции в предыдущем такте управления определяет операцию в последующем такте. Для интерполирования дуги окружности задается номер квадранта и координаты начальной х₀, у₀ и конечной х_k, у_k точек дуги. Для воспроизведения дуги окружности  в положительном направлении (против часовой стрелки) в первом квадранте осуществляется следующий алгоритм управления (рис. 9).

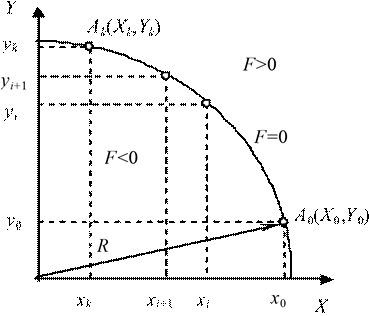
Рис. 9. Круговая интерполяция по методу оценочной функции

Если F_i ≥ 0 (точка находится вне окружности или на ней),  то очередной шаг делается вдоль отрицательного направления оси X,

т. е. х_i+1 = х₁ – 1; если F_i < 0 (точка находится внутри окружности),  то очередной шаг делается в положительном направлении оси Y, т. е. y_i+1 = y_i + 1.

После очередного шага по оси X получим новое значение оценочной функции:

                               F_i+1 = (x_i – 1)² + y²_i – R² = F_i – 2x_i + 1,                        

которое отличается от предыдущего на величину (–2х_i +1). После шага по оси Y новое значение оценочной функции

                                F_i+1 = x_i² + (y_i +1)² – R² = F_i + 2y_i + 1 отличается от предыдущего на величину 2у_i +1.

В таблице 6 для примера приведено вычисление шагов, необходимых для воспроизведения дуги окружности с параметрами К = 20; х_n = 20; у_о = 0:

Таблица 6