Оценочную функцию i-й точки траектории Fi определим в виде
Fi = уiΔх – xiΔy.
Из последнего выражения видно, что если точка, отображающая заданную траекторию, отвечает уравнению прямой, то Fi = 0. Таким образом, заданная прямая делит плоскость на две полуплоскости, в одной из которых оценочная функция Fi положительна, а в другой – отрицательна. В этих полуплоскостях точка находится соответственно выше и ниже заданной прямой. На этом основан алгоритм оценочной функции, при котором с определенной частотой, задаваемой блоком задания скорости, анализируется знак оценочной функции. В зависимости от этого знака выдается сигнал приращения по одной из координат. Масштаб приращений выбирается так, что единица приращения соответствует единице младшего разряда слова системы ЧПУ.
Начало воспроизводимого участка прямой условно совмещается с началом координат. Движение рабочего органа при линейной интерполяции по МОФ показано на рис. 5.
Y
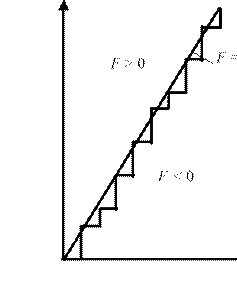
Рис. 5. Линейная интерполяция по методу оценочной функции (элементарные приращения соответствуют одному движению по осям координат)
Определив, что Fi >= 0, выдают один управляющий импульс в направлении координаты X и вновь определяют знак оценочной функции. Если определено Fi < 0, то выдается один импульс для движения в направлении координаты Y. Заметим, что всякий раз после подачи управляющего импульса заново определяется знак оценочной функции. Если после очередного импульса он не изменился, то движение продолжается в том же направлении. Составим выражение для определения очередного значения оценочной функции Fi+1 через ее предыдущее значение Fi. После единичного шага по оси Х(Fi > 0) получим
Fi+1 = уiΔх – (хi+1) Δу = уiΔх – хiΔу – Δу = Fi – Δy.
После единичного шага по оси Y (Fi < 0) запишем
Fi+1 = (уi + 1)Δx – хi Δу = уiΔх – хiΔу + Δx = Fi + Δx.
На этом принципе строится структура линейного интерполятора по МОФ (рис. 6).
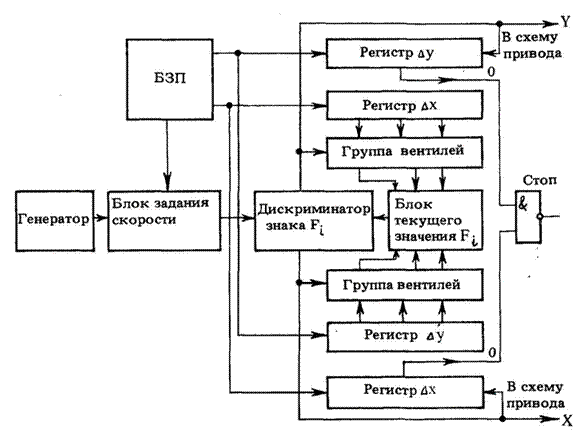
Рис. 6. Функциональная схема линейного интерполятора по методу оценочной функции
Из блока задания программы информация о величинах приращений координат поступает в регистры Δх и Δу, а о величине скорости подачи – в блок задания скорости (БЗС), который может быть построен по принципу управляемого делителя частоты. В регистре Fi хранится текущее значение оценочной функции.
Допустим, что по дискриминатору знак Fi отрицательный. В этом случае импульс, поступающий от БЗС, будет направлен в привод подачи по оси Y, уменьшит содержимое регистра Δу на единицу для определения момента окончания интерполяции; этот же импульс откроет группу вентилей, благодаря чему содержимое регистра ΔX добавится к текущему значению Fi, сформировав новое значение оценочной функции Fi+1.
Если же знак оценочной функции положительный, то аналогичным образом работает нижняя половина схемы. После отработки перемещений в регистрах Δх и Δy образуются логические нули и формируется команда СТОП. Рассмотренный алгоритм МОФ отличается простотой, но имеет недостаток – в нем отсутствует управление одновременно по обеим координатам, что приводит к большой затрате управляющих импульсов и, следовательно, времени интерполяции.
Алгоритм линейной интерполяции по методу оценочной функции может быть усовершенствован путем выдачи приращения по максимальной координате на каждом кванте времен (рис. 7). Максимальной может быть любая из координат X, Y, Z,.... Ход алгоритма, таким образом, зависит от того, по какой из координат задано максимальное приращение. Для того чтобы уменьшить разнообразие алгоритмов управления, целесообразно перейти от реальных координат объекта X, Y, Z,... к абстрактным координатам α, β, γ,..., причем максимальную координату всегда обозначают через α. Это обозначение вводится при интерпретации кадра; обратная операция, т. е. переход от координат α, β, γ,… к координатам X, Y, Z,... осуществляется на выходе системы.
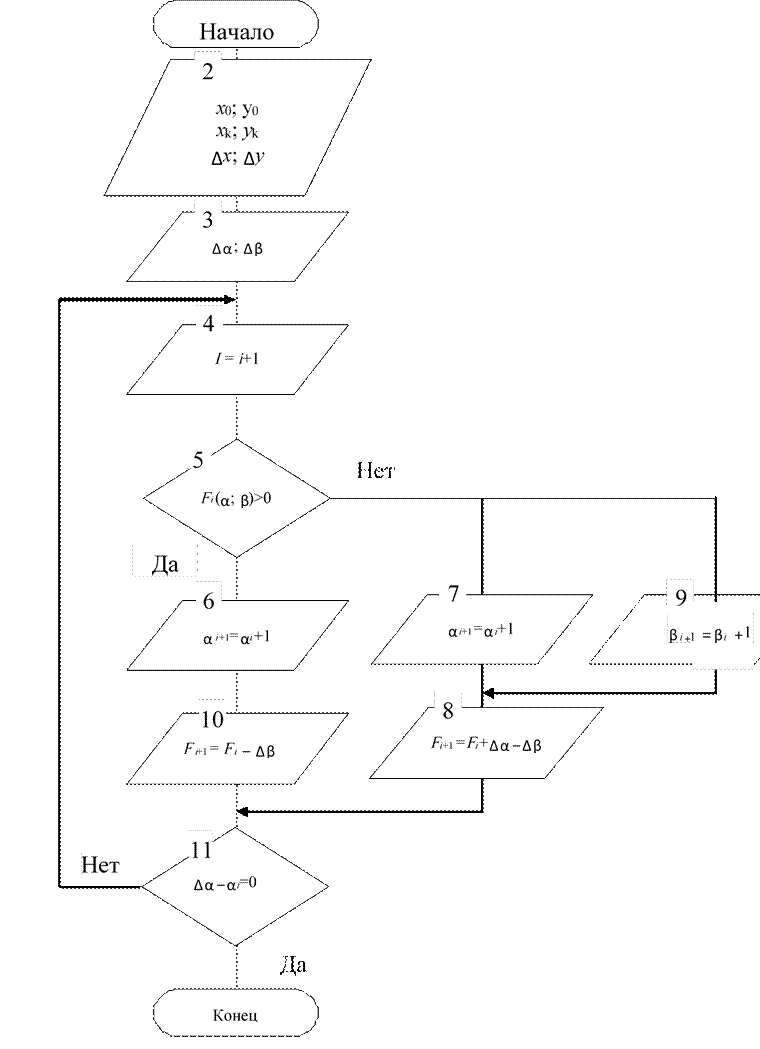
Рис. 7. Усовершенствованный алгоритм линейной интерполяции по методу оценочной функции
Максимальную координату α будем откладывать по оси абсцисс. Тогда при положительном значении оценочной функции (Fi >= 0) осуществляем приращение по оси α, а при Fi < 0 – одновременно по обеим координатам α и β. При Fi > 0 αi+1 = αi + 1; Fi+1 = Fi – Δβ, а при
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.