Преобразование программной информации, интерполяторы. Схемы использования интерполяторов, страница 6

F_i<= 0 получим F_i+1 = F_i + Δα – Δβ, α_i+1 = α_i + 1; β_i+1 = β_i + 1.

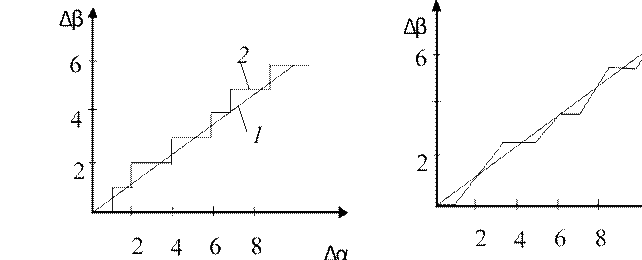
Например, зададимся приращениями в кадре в машинных единицах Δα = 10, Δβ = 6. Траектория движения построена на рис. 8.  Как видно, усовершенствованный алгоритм эффективнее. В данном примере требуется 10 шагов вместо 16 при использовании обычного алгоритма. При отработке траектории прямой под углом 45° скорость движения максимально может вырасти в 2 раза. Контроль окончания отработки кадра можно вести лишь по максимальной координате. Максимальная скорость подачи вдоль одной координатной оси  ν_nmax = h / T_П, где h – значение единичного шага (дискретность подачи); T_П – время реализации алгоритма подачи.

                                                            а)                                             б)

         Рис. 8. Линейная интерполяция по методу оценочной функции  для обычного алгоритма (а) и усовершенствованного (б): 

1 – заданная траектория; 2 – фактическая

Максимальная контурная скорость зависит от числа одновре-

менно работающих координат K: ν_kmax = (h/T_П)√K и имеет наибольшее значение, когда приращения равны.

Оценку быстродействия системы ЧПУ, работающей по методу оценочной функции, дают в виде максимальной частоты выходных импульсов на привод по одной координате: f_max = 1/ T_П. Необходимая частота  f  выдачи сигналов управления (шагов) определяется заданной скоростью подачи ν_n и углами наклона траектории к осям координат

                                                                  1                    vΔα

                                      f =    −                                  ,

                                                                  h         Δα² +Δβ² +Δγ² +...

где Δα, Δβ, Δγ – приращения координат.

Подготовка исходных данных для линейной интерполяции  по методу оценочной функции производится в следующем порядке: 1) определяются приращения в кадре по осям Δx, Δy, Δz в соответствии с которыми назначаются обобщенные координаты α, β, γ, причем максимальной координате присваивается наименование α; 2) определяется частота шагов интерполяции.

Задание 2

Получить график движения рабочего органа при использовании линейного интерполятора, функционирующего по методу оценочной функции. Составить таблицу получения двоичного кода по координатам X и Y с указанием состояния оценочной функции. Пояснить ход расчетов и построений. Приращения координат даны в таблицах 4 и 5: Таблица 4

Задание 3

Получить график движения рабочего органа при использовании линейного интерполятора, функционирующего по усовершенствованному методу оценочной функции. Составить таблицу получения двоичного кода по координатам X и Y с указанием состояния оценочной функции. Данные для расчетов взять из задания 2. Сделать заключение о сравнении двух методов.