Преобразование программной информации, интерполяторы. Схемы использования интерполяторов, страница 2

К первой группе относятся методы оценочной функции и цифрового дифференциального анализатора, ко второй – метод цифрового интегрирования. В системе ЧПУ на базе ЭВМ широко применяется метод цифрового интегрирования. Независимо от принципа действия и реализации интерполятор моделирует в реальном масштабе времени движение изображающей точки по заданной траектории, которое воспроизводится следящими приводами станка или робота.

Исходным является чертеж детали, на основании которого технолог-программист определяет опорные точки. Движение между двумя соседними опорными точками производится по одному и тому же закону – по прямой линии, по окружности или по кривой более высокого порядка. Таким образом, для организации движения между двумя опорными точками необходим один кадр программы. Предположим, требуется смоделировать траекторию движения инструмента, изображенную на рис. 2. Между опорными точками А₁–А₂ движение производится вдоль оси X в отрицательном направлении, между точками А₂–А₃ – вдоль оси Y, между точками А₃–А₄ – вдоль оси X в положительном направлении, между точками А₄–А₅ и А₅–А₆ – по прямой линии с соответствующим наклоном, между точками А₅–А₆ – по дуге окружности.

Y  

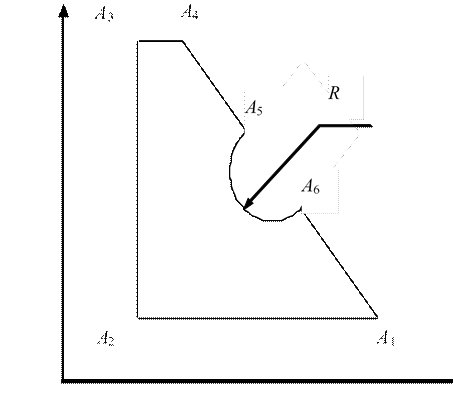
Рис. 2. Траектория движения инструмента

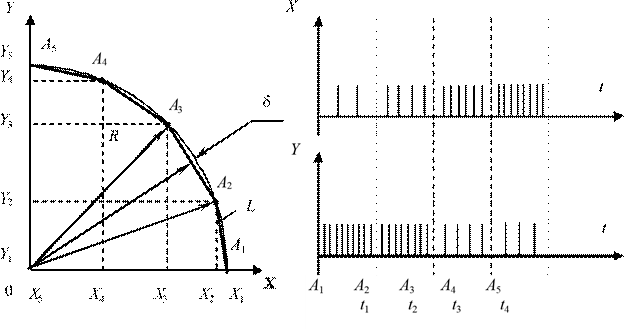
Простейшим интерполятором является линейный. Принципиально сколь угодно сложную кривую можно аппроксимировать с помощью отрезков прямых. Предположим, необходимо смоделировать дугу окружности А₁–А₅, изображенную на рис. 3,а. Она может быть аппроксимирована отрезками прямых А₁А₂, А₂А₃,..., А₄А₅. Чем больше таких отрезков, тем лучше будет приближение к действительной кривой, т. е. тем меньше погрешность δ. Однако большее число отрезков означает более трудоемкое программирование; возрастает также объем программы и программоносителя. Поэтому ограничивающим фактором при аппроксимации является допустимая погрешность δ.  При аппроксимации окружности N участками прямых центральный угол i-го участка найдем из соотношения 

                            α_i =  + (i −1)ϕ= ϕ( + i −1) =ϕ(i −),

где ϕ = ( π/2)/N = π/(2N) – приращение угла на участке аппроксимации.

                           а)                                                 б)

Рис. 3. Аппроксимация дуги окружности отрезками прямых (а)  и последовательности импульсов на выходах линейного интерполятора (б)

Длина участка прямой L и погрешность δ (в первом приближении δ<<R) связаны соотношением

                                                    L = 2·   2Rδ .

С другой стороны, L = 2·R·sinϕ/2, что позволяет определить приращения координат в первом квадранте при известных L и ϕ:

                                           Δx_i = Lcos(−ϕ (i −));

                                                    Δy_i = Lsin(−ϕ(i −)).

Скорость движения на траектории ν₁ определяется требованиями технологии. Цикл работы интерполятора, т. е. время отработки кадра

                                 Δt_i = t_i+1 – t_i =     (Δx_i )² + (Δy_i )² v_i .

Тогда скорость движения по координатам:

                                                                 Δxi =       Δxi              vi =Δxi vi;

                                   vxi =Δy              2              2              Δki

                                                                       i             Δxi +Δyi

                                                                 Δyi =       Δyi              vi =Δyi vi;

                                   vyi = Δt_i             Δx_i2 +Δy_i2             Δki

За время i-го цикла по координате X должно быть выдано 

N_xi = Δx_i/ h импульсов с частотой

N^xi Δxivi   f = = ,

xi

                                                                                       Δti         hΔk_i

а по координате Y с частотой

Δyivi            f yi =  ,

hΔk_i

где h – цена деления импульса.

Обычно приращения координат подаются на вход интерполятора в двоичном коде, что позволяет записать

                              fxi          an,x 2n + an−1,x 2n−1 +...+ a1,x 21 + a0,x 20          Kx

          =      =      , n          n−1        1             0

                              f yi        an, y 2 + an−1, y 2      +...+ a1, y 2 + a0, y 2       K y