Вибрационные машины. Научно-техническое обоснование. Расчеты и разработка конструкции изделия, страница 9

.               (2. стр 75.)

Число ремней передачи [6]:

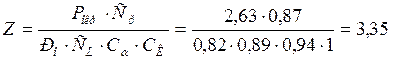;                             (2. стр 76.)

где - окружное усилие, кН;

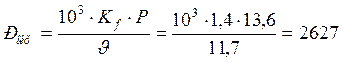Н = 2,63 кН

где  - коэффициент динамичности нагрузки и режима работы,

= 1,4 [5.табл. 14.6];

P – передаваемая мощность;

 - скорость ремня.                   

- усилие передаваемое одним ремнем,Н  = 0,82 кН[5, рис. 14.10];

=0,89- коэффициент учитывающий длину ремня [6.табл.2.2.5];

=094- коэффициент учитывающий угол обхвата [6.табл.2.2.4];

=1- коэффициент учитывающий скорость ремня [6.табл.2.2.2.].

- коэффициент режима работы, при двухсменной работе = 0,87.

Принимаем 4 ремня.

2.4.2. Расчет зубчатой передачи.

Рассчитаем основные параметры зубчатой передачи с помощью, которой передается крутящий момент от одного вала к другому(в вибраторе):

Данная зубчатая передача состоит из двух колес, одинаковых диаметров.

момент на зубчатом колесе.

коэффициент зубчатого колеса.

частота вращения 1-го вала вибратора.

частота вращения 2-го вала вибратора.

Материал колес - Сталь 40ХН прошедшая поверхностную закалку,

НRC = 50…55,  и .

Принимаем предварительно коэффициент нагрузки  т.к. колеса расположены на краях валов и поэтому валы могут испытывать изгибающий момент.

Передаточное число

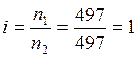
По графику (2, рис. 10.12) по , , , допускаемому контактному напряжению для материала колеса , и для прямозубых колес находим межосевое расстояние  и округляем его, по ГОСТу 2185-66 принимаем .

Принимаем модуль по соотношению:

Принимаем по ГОСТу9563-60

Суммарное число зубьев:

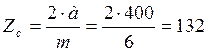
Число зубьев 1-го колеса:

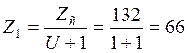
принимаем

Поскольку колеса равны, то число зубьев второго колеса будет равно:

Фактическое передаточное число:

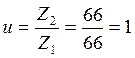
Основные размеры колес:

Ширина колес:

Окружная скорость:

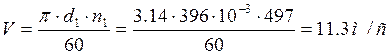
По (2, табл. 10.8) принимаем 9-ю степень точности.

Уточняем коэффициент нагрузки. По (2, табл. 10.11) в зависимости от 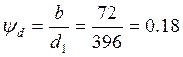 и 9-ой степени точности находим .

По формуле подсчитаем:

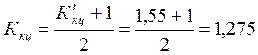
По (2, табл. 10.9) для скорости 11,3 м/с при твердости до НRC = 650 для

9-ой степени точности находим .

Коэффициент нагрузки:

Проверяем расчетные контактные напряжения по формуле:

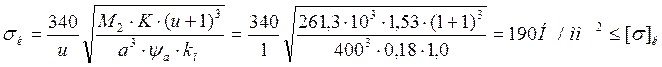
Проверка прочности зубьев на изгиб:

Находим произведения :

Расчетное напряжение изгиба в опасном сечении зуба колес:

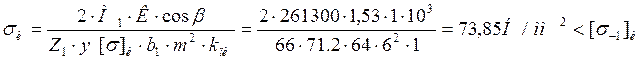, следовательно, прочность на изгиб обеспечена.

2.5. Расчет эксцентрикового вала.

Расчёт произведём для первого вала вибратора, так как он более нагружен.

Принимаем материал вала сталь 40X. []=320 МПа, =600 МПа, НВ=260 с последующей термообработкой.

Вращающий момент

 = 261,3 Нм.

Сила передаваемая клиноременной передачей

Fp== 2630 Н.

Силы, действующие на зубчатое колесо:

Окружная сила:

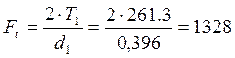 Н.

где   -  делительный диаметр, м.

Радиальная сила:

 Н.

где  - угол зацепления (для прямозубых передач ).

Осевая сила:

 Н.

где  - угол наклона линии зуба на делительном цилиндре. - у прямозубых колес.

Определяем опорные реакции в опорах А и В в горизонтальной плоскости.

∑М_А= 0: 

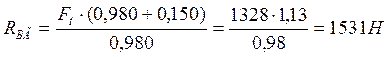
∑М_В= 0:

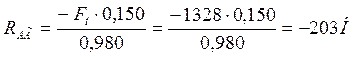
Проверяем ∑Y = 0

 − реакции определены, верно.

Определяем опорные реакции в вертикальной плоскости :

∑М_А= 0: 

     

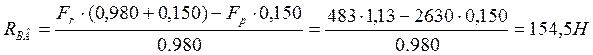
∑М_В= 0:

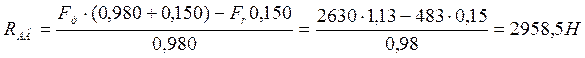
Проверяем ∑Z= 0 

Реакции определены верно.

Определяем суммарные опорные реакции:

Построение эпюр  ,  ,   ,    ,   .

        

Определяем суммарные изгибающие моменты:

Определяем суммарные эквивалентные моменты:

Определяем расчётный диаметр вала

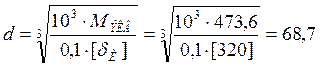 мм.

Согласно ГОСТ 6636-69 принимаем под конец вала со шкивом d = 70мм, под подшипник d = 110 мм, под пластины d = 160мм.

 2.6. Расчет шпоночных соединений.

Для соединения валов с деталями, передающими вращение, используем призматические шпонки.

Проверка шпонки на смятие рабочих граней должна удовлетворять условию [3 стр.236] :