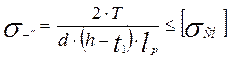Вибрационные машины. Научно-техническое обоснование. Расчеты и разработка конструкции изделия, страница 10

                                                    (11.1)

где  Т - передаваемый вращающий момент;

d - диаметр вала в месте установки шпонки;

h - высота шпонки;

t₁ - глубина шпоночного паза на валу;

l_р - рабочая  длина  шпонки,  для  шпонок  со  скругленными торцами   l_р  =  l - b  ( b - ширина шпонки);

[_см ] - допускаемое напряжение смятия; при стальной ступице

[_см ]  = 100 МПа.

Расчет шпоночного соединения первого вала вибратора со шкивом.

Диаметр вала d = 70 мм, вращающий момент Т = 261,3•10³ Н•мм.

По ГОСТ 23360-78 подбираем призматическую шпонку с размерами сечения: b = 20 мм, h = 12 мм, t₁ = 7,5 мм. Длину шпонки принимаем из стандартного ряда l = 95 мм. Тогда  l_р = 95 - 20 = 75 мм.

Напряжения смятия

_см = 2 • 261,3•10³ / [ 70 • (12 – 7,5) • 75 ] = 22,1 МПа.

Условие прочности  шпонки  20 х 12 х 95  выполняется

Рис.9. Соединение с призматической шпонкой

2.7. Подбор подшипников.

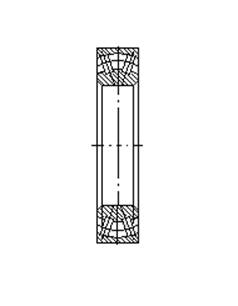
Рис. 10. Роликовый радиальный двухрядный сферический подшипник.

Выбираем по ГОСТ 22428-90 роликовые радиальные двухрядные сферические подшипники с параметрами: d=110 мм D=200 мм, В=53 мм.  Подшипник 3522 ГОСТ 5721-75.

Эквивалентная динамическая нагрузка Р

Р=(ХVF)КК=483*1*1*1,2*1=580 Н

Где V=1-коэфициент вращения;

Х=1-коэфициент радиальной нагрузки;

F=483 Н - радиальная нагрузка;

К=1,2 – коэффициент учитывающий динамичность внешней нагрузки;

К=1-коэфициент, учитывающий влияние температуры подшипникового узла.[1, 353]

Номинальная долговечность подшипника в миллионах оборотов

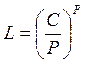
где Р=3-степеной показатель

С=108 кН – динамическая грузоподъёмность.

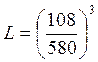=6,46 млн. об.

долговечность подшипника в часах

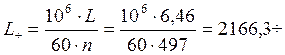
Расчётная динамическая радиальная грузоподъёмность

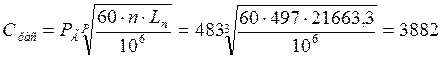 Н

Пригодность ранее выбранного подшипника следует из условия

, Н;

 Н.

2.8. Расчет амортизаторов.

В большинстве вибрационных машин амортизаторы находятся под действием установившихся знакопеременных нагрузок, за исключением моментов пуска и остановки машины, когда вследствие перехода через резонанс амплитуда деформации амортизаторов может значительно превосходить амплитуды стационарных процессов.

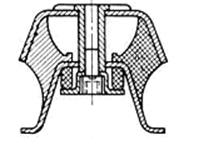
Рис.11 Резинометаллический амортизатор.

Детали такого типа широко используют в качестве элементов рессорной подвески тележек подвижного состава, амортизации железнодорожных мостов, виброизоляции горно-шахтного и металлургического оборудования и т.д.

Отношение площади основания детали, соприкасающейся со сжимающими поверхностями, к площади ее боковой поверхности называется фактором формы Ф.

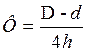                                                                                      [стр.98, 10 ]

Для резинометаллических деталей фактор формы Ф=1,0 ÷ 1,25. [стр.99,10 ]

Зададимся высотой h и найдем остальные геометрические размеры резиновой втулки. Пуст h=8 см.

        

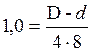
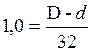
d=75 мм.

D=75+32=107 мм.

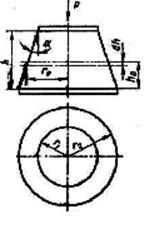
Рис.12 Схема к расчету резинометаллических деталей типа усеченного конуса.

Если резиновый элемент представляет собой усеченный конус (рис.12), нагруженный осевой силой Р, то напряжение сжатия будет переменной величиной, достигающей максимального значения у меньшего основания с радиусом r1 и минимального – у большего основания с радиусом r2. Напряжение в некотором промежуточном сечении с радиусом r0 составит

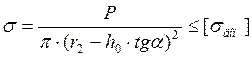                                                  [стр.104, 10 ]

 [табл.3, стр.53,10]

r1=d/2=75/2=37,5 мм. – радиус меньшего основания;

r2=D/2=107/2=53,5 мм. – радиус большего основания;

h0=40мм.

 - наружная осевая сила;

где  - масса двигателя;

 - ускорение свободного падения;

 - коэффициент динамичности.

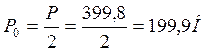 , т.к. амортизатора два.

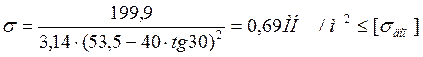
Полная осадка Δ конического элемента высотой h составит

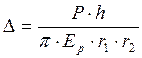,                                                                      [стр.104, 10 ]