Определение токов и напряжения на конденсаторе после коммутации в данной электрической цепи второго порядка сложности, страница 5

Для получения тока  воспользуемся теоремой разложения:

,

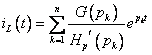где  - число корней  полинома знаменателя . Дальнейшее решение представим поэтапно:

1.  Определим корни  из уравнения

.

Решив его, находим:

 ,  ,  .

2.  Найдём полином :

3.  Вычислим коэффициент для корня  :

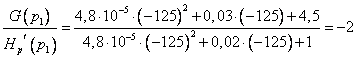А

4.  Вычислим коэффициент для корня  :

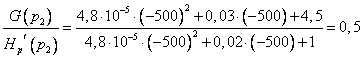А.

5.  Вычислим коэффициент для корня  :

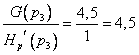А.

6.  Составим выражение для искомого тока (в амперах):

А.

Как и ожидалось, это выражение совпадает с формулой (5) для , полученной классическим методом. Токи остальных ветвей и напряжение  находятся аналогично и совпадают с полученными ранее.

3. Метод переменных состояния.

При составлении уравнений состояния  несложных цепей для уменьшения промежуточных преобразований рекомендуется для -элемента использовать переменные  и  (для напряжения), а для -элемента -  и  (для тока). Также по возможности следует записывать уравнения так, чтобы в каждое из них входило не более одной производной от переменной состояния. После составления уравнений Кирхгофа, из них исключаются все алгебраические переменные, т.е. переменные не являющиеся переменными состояния.