Определение токов и напряжения на конденсаторе после коммутации в данной электрической цепи второго порядка сложности, страница 3

Решение однородного уравнения, называемое переходящим током, имеет в рассматриваемом случае вид: ,

где  и  - постоянные интегрирования;  и  - корни характеристического уравнения: .

Решая это уравнение, находим корни:

,

С учётом результатов, полученных на этапе 2, решение (3) принимает следующий вид:

 (4).

Для производной этой функции имеем:

.

Этап 6. Определение постоянных интегрирования.

Используя начальные условия, строим систему уравнений для определения  и :

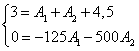, откуда ,  .

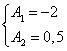Т.е. решив  эту систему, находим  и , после подстановки этих величин в правую часть (4) получаем ответ в амперах:

. (5)

Этап 7. Определение остальных токов и построение их графиков. Из системы (1) и с учётом (5) находим токи в амперах:

и напряжение на -элементе в вольтах:

.

В соответствии с этими формулами были построены графики изменения токов и напряжения .