Определение токов и напряжения на конденсаторе после коммутации в данной электрической цепи второго порядка сложности, страница 4

2. Операторный метод.

Как и при использовании классического метода, предварительно следует найти начальные условия для переменных состояния:

А,                      В.

Эти величины используются при формировании уравнений цепи в операторной форме. Согласно законам Кирхгофа, для данной цепи, можно составить следующую системы уравнений в операторной форме:

,

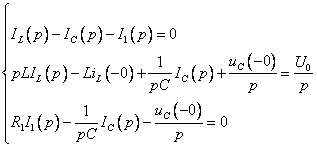После подстановки числовых параметров цепи, эта система принимает вид:

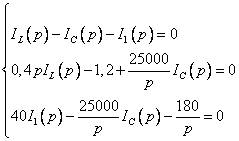
Если для упрощения решения задачи классическим методом целесообразно сведение системы к уравнениям относительно тока  или напряжения , непрерывных при коммутации, то при решении операторным методом это не важно, потому что начальные условия автоматически учитываются при записи системы уравнений. В нашем случае сведём систему к уравнению для тока , чтобы сравнить полученное решение с ранее найденным ответом:

,

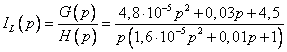где  - полином числителя, а  - полином знаменателя.

Также желательно проконтролировать правильность полученного выражения с помощью предельных соотношений:

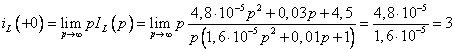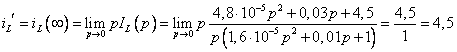А

А.

Вычисленные здесь  и  совпадают со значениями, полученными в классическом методе.