

















ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
Истинное электрическое поле в веществе микрополе меняется резко как в пространстве, так и во времени.
![]() Под
электрическим полем в веществе будем понимать пространственно усредненное микрополе
E! =
E!микро .
Под
электрическим полем в веществе будем понимать пространственно усредненное микрополе
E! =
E!микро .
Влияние вещества на поле: При внесении любого вещества в электрическое поле в веществе происходит смещение положительных и отрицательных зарядов, что приводит к частичному разделению этих зарядов. Появляются нескомпенсированные заряды различного знака. Это явление называется электростатической индукцией, а появившееся в результате разделения заряды индуцированными зарядами.
Поле внутри и снаружи
проводника: Внутри проводника E! = 0. Поле у поверхности проводника
En =
![]() σ
. Если σ>
0, то и En > 0, т.е. вектор
σ
. Если σ>
0, то и En > 0, т.е. вектор
ε0
E! направлен от поверхности проводника совпадает с нормалью n!, если σ< 0, то En < 0 вектор E! направлен к поверхности проводника.
По мере удаления от системы зарядов эквипотенциальные поверхности становятся все более близкими к сферическим, линии вектора E! приближаются к радиальным, а поле становится близким к полю точечного заряда q полному заряда данной системы.
Силы, действующие на поверхность проводника:
Пусть заряженный участок поверхности проводника граничит с вакуумом, тогда: ∆F =σ∆ ⋅S E0 , где σ∆S заряд этого элемента, E0 напряженность поля, создаваемого всеми остальными зарядами системы в точке нахождения заряда σ∆S .
Уравнения Пуассона и Лапласа:
![]() уравнение Пуассона,
где ∇2 оператор Лапласа (лапласиан);
в декартовых координатах он имеет вид:
уравнение Пуассона,
где ∇2 оператор Лапласа (лапласиан);
в декартовых координатах он имеет вид: 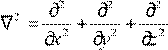 .
.
Если между проводниками нет зарядов, то ∇2ϕ= 0 уравнение Лапласа. Электроемкость. Конденсаторы.
Электроемкость (емкость) уединенного проводника: C = ϕq .
Емкость зависит от размеров и формы проводника.
Конденсатор система проводников, обладающая емкостью значительно большей, чем уединенный проводник: C = ϕq емкость конденсатора, где
U напряжение (разность потенциалов между обкладками).
![]() Емкость
плоского конденсатора: C
= εεh0S .
Емкость
плоского конденсатора: C
= εεh0S .
Емкость сферического конденсатора: C = 4πεε0 bab− a , где a и b радиусы внутренней и внешней обкладок конденсатора.
Емкость цилиндрического
конденсатора: C =
![]() 2πεε
l ,
где l длина конденсатора,
a и b радиусы внутренней и наружной
цилиндрической обкладок.
2πεε
l ,
где l длина конденсатора,
a и b радиусы внутренней и наружной
цилиндрической обкладок.
Диэлектриками (или изоляторами) называют вещества, практически
не проводящие электрического тока. ![]() i поляризованность диэлектрика.
i поляризованность диэлектрика.
![]() P! =
n p! ,
где n =
∆∆NV концентрация молекул.
P! =
n p! ,
где n =
∆∆NV концентрация молекул.
![]() p! =
(∑∆Np!i )
средний дипольный момент одной молекулы.
p! =
(∑∆Np!i )
средний дипольный момент одной молекулы.
Если диэлектрик изотропный, а E! не слишком велико, то P! = χε0E! , где χ диэлектрическая восприимчивость вещества.
Теорема Гаусса для вектора P! : "∫ PdS! ! = −qвнутр′ поток вектора P! сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному заряду диэлектрика в объеме, охватываемом поверхностью S .
∇⋅! !P = −ρ′ дифференциальная форма теоремы Гаусса, где ρ′ объемная плотность избыточного связанного заряда.
"∫ε0EdS! ! = (q +q′)внутр теорема Гаусса, где q и q′ сторонние и связанные заряды, охватываемые поверхностью S .
"∫(ε0E! !+ P dS) ! = qвнутр ,
D =ε0E! !+ P ,
"∫ DdS! ! = qвнутр теорема Гаусса для поля вектора D! .
∇! !D = ρ дифференциальная
форма теоремы Гаусса. Связь между векторами ![]() :
:
D! =ε χ0 (1+ )E! или D! =εε0E! , где ε= +1 χ диэлектрическая проницаемость. Энергия электрического поля:
W ![]() q энергия взаимодействия
системы точечных зарядов, где qi
i-й заряд системы,
ϕi потенциал, создаваемый
в точке нахождения i-го
q энергия взаимодействия
системы точечных зарядов, где qi
i-й заряд системы,
ϕi потенциал, создаваемый
в точке нахождения i-го
заряда.
W ![]() dV , где ρdV = dq, ϕ
потенциал, создаваемый всеми зарядами системы в элементе объемом dV .
dV , где ρdV = dq, ϕ
потенциал, создаваемый всеми зарядами системы в элементе объемом dV .
W = q2ϕ ϕ= C2 2 = 2qC2 энергия уединенного проводника.
W = qU2 = CU2 2 = 2qC2 энергия конденсатора.
![]() !!
!!
W dV dV энергия однородного электрического поля, заполняющего объем V .
ω=
εε![]() E2 =
ED!! объемная
плотность энергии. Эта формула справедлива только в случае изотропного диэлектрика,
для которого выполняется соотношение P! = χε0E! .
E2 =
ED!! объемная
плотность энергии. Эта формула справедлива только в случае изотропного диэлектрика,
для которого выполняется соотношение P! = χε0E! .
A =
![]() работа на поляризацию
единицы объема диэлектрика.
работа на поляризацию
единицы объема диэлектрика.
ЗАДАЧИ
Нахождение потенциала:
1. Система состоит из двух концентрических проводящих сред, причем на внутренней сфере радиуса R1 помещен заряд q1. Какой заряд q2 следует поместить на внешнюю сферу радиуса R2 , чтобы потенциал внутренней сферы стал равен нулю.
Решение 1:
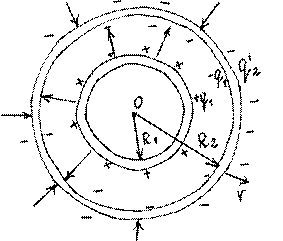 Заряд распределяется симметрично. Чтобы внутри второй сферы было E! =
0 надо, чтобы все
силовые линии, начинающиеся на заряде +qi , заканчивались на
внутренней поверхности сферы R2 ,
т.е. на ней распределится заряд −q1. А на внешней поверхности сферы R2 будет заряд
Заряд распределяется симметрично. Чтобы внутри второй сферы было E! =
0 надо, чтобы все
силовые линии, начинающиеся на заряде +qi , заканчивались на
внутренней поверхности сферы R2 ,
т.е. на ней распределится заряд −q1. А на внешней поверхности сферы R2 будет заряд
q2′ = q2 + q1, который и создает поле вне системы (поле шара вне шара
![]() совпадает с полем
точечного заряда), т.е. ϕ1(r
>R2 ) =
4πεq′20r .
совпадает с полем
точечного заряда), т.е. ϕ1(r
>R2 ) =
4πεq′20r .
![]() Внутри сферы
R2 (R1<r <R2 ): ϕ2 (R1<r <R2 )= q1 +ϕ0 ,
Внутри сферы
R2 (R1<r <R2 ): ϕ2 (R1<r <R2 )= q1 +ϕ0 ,
4πε0r
![]()
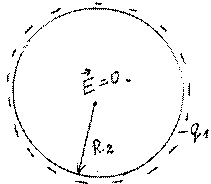 где 4πεq10r потенциал, создаваемый зарядом q1 на сфере R1, ϕ0 постоянный потенциал,
созданный зарядом −q1 на сфере R2 .
где 4πεq10r потенциал, создаваемый зарядом q1 на сфере R1, ϕ0 постоянный потенциал,
созданный зарядом −q1 на сфере R2 .
![]() На границе r = R2 : ϕ ϕ1 = 2 или 4qπε1 +0qR22 = 4πεq10R2 +ϕ0
На границе r = R2 : ϕ ϕ1 = 2 или 4qπε1 +0qR22 = 4πεq10R2 +ϕ0
![]() или ϕ0 = 4πεq20R2 .
или ϕ0 = 4πεq20R2 .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.