Решение:
По определению емкость C = ϕq .Найдем потенциал ϕ проводника,
мысленно сообщив ему заряд q: ϕ= ∞∫0 E drr = 4πε ε1 0 ∫ba qr2 dr + 4πε1 0 ∞∫b rq2 dr .
После интегрирования этого выражения получим:
ϕ= q0 1a +εb−1 , C = 1+4(επεε−01)aa b . 4πεε
Ответ:
C =
1+4(επεε−01)aa b .
7.
Сферический конденсатор с радиусами обкладок a и b , где a < b , заполнен изотропным, но неоднородным диэлектриком,
проницаемость которого зависит от расстояния r до центра системы как ε=α
r , где α
постоянная. Найти емкость такого конденсатора.
Решение:
Согласно определению емкости конденсатора C = Uq задача сводится к нахождению разности потенциалов U при заданном заряде q:
b
U = ∫Edr ,где предполагается, что внутренняя обкладка имеет заряд q > 0.
a
Определим E с помощью теоремы Гаусса для вектора D! :
4πr D2 = q , E = εε πε εD0 = 4 1 0 qr2 = 4πεα1 0 qr .
После подстановки последнего выражения в исходный интеграл и соответствующего интегрирования найдем:
U = q0 ln b , C = ln4πεα(b a0 ) .
4πεα a
Ответ: C =
.
Энергия электростатического поля:
8. Система состоит из двух концентрических металлических оболочек радиусами R1 и R2 с соответствующими зарядами q1 и q2 . Найти собственную энергию W1 и W2 каждой оболочки, энергию Wвз взаимодействия оболочек и полную электрическую энергию W данной системы, если R2 > R1.
Решение:
Собственная
энергия каждой оболочки равна q2ϕ, где ϕ
потенциал оболочки, обусловленный только зарядом q на ней, т.е. ϕ=
4πεq0R , где R радиус оболочки. Таким образом,
собственная энергия каждой оболочки
W1,2 =
4πε1 0 2qR12,21,2 .
Энергия взаимодействия заряженных оболочек равна заряду одной из них, умноженному на потенциал ϕ, который создает заряд другой оболочки в месте нахождения заряда q: Wвз = qϕ.
В нашем случае (R2 > R1): Wвз = q1 4πε1 0 Rq22 = 4πε1 0 q qR1 22 . Полная электрическая энергия системы
W =W1 +W2 +Wвз = 4πε1 0 2qR121 + 2qR222 + q qR1 22 .
Ответ: W1,2 = 4πε1 0 2qR12,21,2 ,
Wвз = 4πε1 0 q qR1
22 , W = 4πε1 0 2qR121 + 2qR222 + q qR1
22 .
9. Два небольших
металлических шарика с радиусами R1
и R2 находятся в вакууме на
расстоянии, значительно превышающем их размеры, и имеют некоторый определенный суммарный
заряд. При каком отношении q
q12
зарядов на шариках электрическая энергия системы будет минимальной? Какова при этом
разность потенциалов между шариками?
Решение:
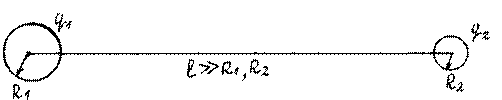
Электрическая энергия системы складывается из собственных энергий заряда на каждом проводнике и энергии их взаимодействия. На большом удалении шарики можно считать уединенным и
Wiсобст = qi2 , Ci = 4πε0Ri емкость шара.
2Ci
На большом расстоянии шарик q2 можно считать почти точечным и он создает на шарике 1 потенциал ϕ12 = 4πεq20l ,
т.е. Wвз = q1 1ϕ 2 = 4q qπε1 20l .
Полная энергия W = 4πε1 0 2qR121 + 2qR222 + q q1l 2 .
Подставляя q2 = q −q1, ищем минимум энергии (q = const суммарный заряд).
∂W ∼ 22Rq11 + 2(q −2qR12)( )−1 + q −l2q1 ,
∂q1
последним слагаемым можно пренебречь, т.к. l $ Ri , т.о.
R1 R2 .
Условие минимума энергии: qq12 = RR12 .
Потенциалы шариков ϕ1 = Cq11 +ϕ12 , ϕ2 = Cq22 +ϕ21, ϕ12 и ϕ21 малы, т.к. пропорциональны 1l , можно пренебречь, Cq11 , Cq22 потенциалы
изолированных шариков, т.е. ϕ ϕ1 − 2 = 4πε1 0 Rq11 + Rq22 = 0 .
Ответ: ϕ ϕ1 − 2 = 0.
10. Заряд распределен по объему шара радиуса R , уединенного в вакууме,
n с плотностью ρ ρ= 0 Rr , где r расстояние до центра шара, ρ0 постоянная. При каком показателе n энергия поля внутри шара будет равна энергии поля вне шара?
Решение:
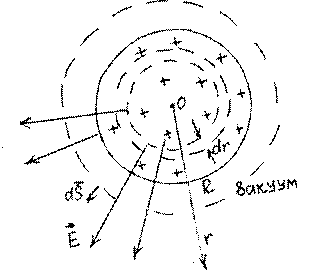Найдем сначала зависимость E r( ).
По теореме Гаусса "∫ EdS! ! = ∑ε0q , где ∑q суммарный заряд внутри сферической поверхности радиуса r . Чтобы найти этот заряд, разбиваем шар на сферические слои толщиной dr с объемом dV = 4πr dr2 и
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.