Электрическое поле в веществе. Основные определения и формулы. Проводник в электрическом поле. Силы, действующие на поверхность проводника, страница 3

Решение:

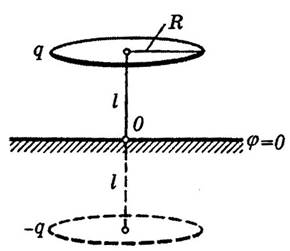Легко догадаться, что в соответствии с методом изображений фиктивный заряд −q должен быть расположен на таком же кольце, но по другую сторону проводящей плоскости. Действительно, только в этом случае потенциал на средней плоскости между этими кольцами равен нулю, т.е. совпадает с потенциалом проводящей плоскости.

Для нахождения σ в точке 0 необходимо найти напряженность E поля в этой точке.

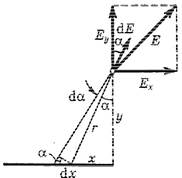Вначале найдем поле на оси равномерно заряженного кольца, а затем удвоим результат. В случае тонкого равномерно заряженного кольца вектор E должен быть направлен по оси кольца. Выделим на кольце около точки А элемент dl . Запишем выражение для составляющей dE_z от этого элемента в точке С: dE_z = _4πε¹ 0 ^λ_r^dl₂ cosα, где λ= 2παq .

Для всех элементов кольца r и α будут одними и теми же, поэтому интегрирование этого выражения сводится просто к замене λdl на q. В результате E = ₄πε^q 0 (_a2 ₊^z_z2 )32 .

В нашем случае, в результате σ ₌         ^ql        ₃ .

2π(R2 +l2 ) 2

Потенциал в центре кольца равен алгебраической сумме потенциалов в этой точке, создаваемых зарядами q и −q: ϕ= _4πε¹ 0 ^_ _R^q − _R2^q_+4l2 _^.

Ответ: σ = 2        2ql 2 32 , ϕ= 4πε1 0  Rq − R2q+4l2 .

π(R +l )

Емкость, конденсатор:

4.  Пластины плоского конденсатора, расстояние между которыми равно d , замкнули накоротко проводом и поместили между ними, на расстоянии d_{1 =} ^d4 от одной из них точечный заряд q. Какой заряд будет индуцирован на второй пластине?

Решение:

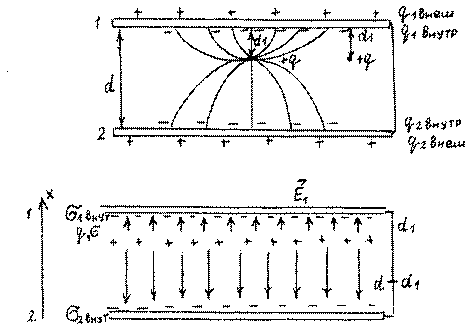
Если на том же расстоянии d₁ от пластины 1 поместить еще один заряд q, то индуцированный на внутренней поверхности пластин заряд q_1,2внут удвоится, но его отношение _q^q12^внутвнут =η не изменится. Т.е. не изменится это отношение если заряд q равномерно размазать на плоскости параллельной плоскости конденсатора.

Тогда поле между зарядами внутри конденсатора однородно и разность потенциалов между пластинами

                   d d− ₁                                     d

ϕ ϕ₂ − ₁ = ∫ E dx_2x + ∫ E_1x = E d_{1 1} − E₂ (d −d₁)= 0                    пластины имеют одинаковый

0         d d− ₁ потенциал т.к. замкнуты накоротко. (E_2x = −E₂ = const E, _1x = E₁ = const). Но вблизи заряженного проводника E_{1 =} ^σ_ε^1внут0    , E_{2 =} ^σ_ε^2внут0                   , и кроме того индуцированные заряды равны в сумме −q:

σσ σ1внут= −d(1 =1внутσ2внут+σ(2dвнут−)d1) −(σ σ+         2внут )d1 =σ2внут (d −d1), т.е. σ2внут = −σdd1 .

Тогда σ_1внут = −(σ σ+   _2внут )= −σ^_1− ^d_d¹ _^_ = −σ^{d −}_d^d1 , т.е. отношение зарядов,

индуцированных на внутренних пластинах _q^q12^внутвнут = _σ^σ12^внутвнут ^{= d} _d⁻1^d1 и q_2внут = −q ^d_d¹ = − ^q₄ . Т.к. потенциал пластин одинаков, то на внешней сторон их поверхности окажется одинаковый заряд q1внеш = q2внеш = q2 − (q1внут +2q2внут ) .

В результате заряд на второй пластине q2 = q2внут + q2внеш = q4 , q1 = − q4 .

Ответ: q2 = q2внут + q2внеш = q4 .

5.  Сферический конденсатор с радиусом внутренней обкладки R₀ и радиусом внешней обкладки R =  заполнен диэлектриком, диэлектрическая проницаемость которого изменяется с расстоянием r от центра конденсатора по закону ε= _R^r0 . Найти емкость такого конденсатора.

Решение:

Пусть на внутренней обкладке находится заряд q. Окружив ее сферической поверхностью радиуса r и используя теорему Гаусса для векторов электрической индукции D^! , легко найти, что D = ₄π^q_r2 . Так как ε зависит только от r (случай сферической симметрии), то напряженность поля вычисляется по формуле E ₌ ^D . Тогда разность потенциалов между

εε₀

обкладками R R qR           dr        2q        .

                                                    0                                ₀                  0                                0    0

Отсюда емкость конденсатора C  .

Ответ: C =  .

6.  Найти емкость шарового проводника радиусом a, окруженного примыкающим к нему слоем однородного диэлектрика с наружным радиусом b и проницаемостью ε.