Электрическое поле в веществе. Основные определения и формулы. Проводник в электрическом поле. Силы, действующие на поверхность проводника, страница 2

По        условию        на        внутренней        сфере

ϕ2 (r = R1)= 0 = 4πεq10R1 + 4πεq20R2 = 0 или q2 = −q1 RR12 .

Решение 2:

Потенциал  это разность потенциалов между данной точкой и бесконечно удаленной точкой, где ϕ_∞ = 0 .

Тогда ϕ ϕ ϕ ϕ1 ≡ 1∞ = 12 + 2∞ = Cсф кондq.1 . + Cqшара′2 = 0, где C_{сф конд. .}  емкость сферического конденсатора с обкладками R₁ и R₂ , C_шара  емкость уединенного шара радиусом R₂ .

4πε0 qR1R R2 1− 2R1 + qπε1 + q2 = 0 , т.е. q1 RR R2 2− R11  + q1R+2q2 = 0, ⇒ q2 = −q1 RR12 .

                               4    0R2                                    

Ответ: q₂ = −q₁ ^R2 .

R₁

Метод изображений:

2. Точечный заряд q находится на расстоянии r от тонкой бесконечной проводящей плоскости. Найти заряд, индуцированный на плоскости в круге с радиусом R и с центром в точке, расстояние от которой до заряда q минимально. Чему равна энергия системы (какой потенциал создает индуцированный на плоскости заряд в точке расположения заряда q). Какую работу надо совершить, чтобы медленно отодвинуть точечный заряд от плоскости на очень большое расстояние?

Решение:

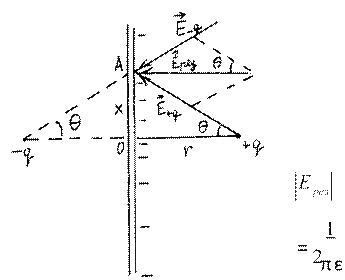Используем метод зеркального изображения. Два заряда +q и −q создадут в точке А на поверхности плоскости результирующее

поле

= E_+q cosθ+ E_−q cosθ = 2 ¹ ₂ ^q ₂ cosθ = 4πε0 r + x

                                                                                                     qr         3 = σин                                                                                                                                            

0 ( r2 + x2 ) ^ε0

поле вблизи проводника;

cosθ = 2^r 2 , ( r + x )

E!_рез ⊥ поверхности плоскости.

Т.е. распределение индуцированного поверхностного заряда имеет вид (с

учетом знака заряда): σ_ин ^−qr ₃ . 2π(r2 + x2 ) 2

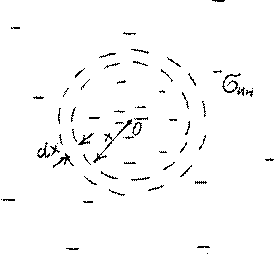Тогда в кольце радиусом x и толщиной dx наведен заряд  dqин =σ πин ⋅2 xdx = − qrxdx 3 , (r2 + x2 ) 2

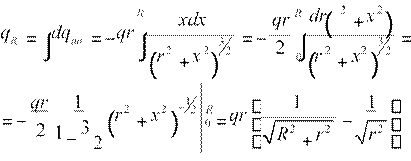
т.е. в круге радиуса R с центром в 0 индуцирован         заряд:

0

или qR =−q1−     2r 2 .

                                   R +r 

Естественно при R → ∞ на всей плоскости индуцирован заряд q_ин = −q.

Энергия системы равна W = ∫dq_{ин пов}ϕ + qϕ_q , где ∫dq_{ин пов}ϕ = 0  энергия самодействия индуцированного заряда на поверхности равна нулю, т.к. потенциал бесконечной проводящей поверхности равен нулю, qϕ_q  энергия взаимодействия точечного заряда q и индуцированного заряда. ϕ_q  это потенциал, создаваемый

индуцированным зарядом в точке расположения заряда q.

dϕ_{q =} ^{σ πин ⋅2} ₂ ^xdx₂  это потенциал, создаваемый индуцированным зарядом

4πε0 r + x

кольца с площадью 2πxdx , т.е.

ϕq = ∫dϕq = ∫∞0 4πε0−(qrxdxx2 + r2 )2 = −8πεqr 0 ∫∞0 d x(x(2 +2 +r2r)22) = 8πεqr 0 x2 1+r2 0∞ =ϕq = − 8πεqr0r2 = −8πεq0r

А энергия взаимодействия W_вз = − ^q2         = −   ^q    .

                                                                                   8πε₀r      8πε₀r

Заметим, что в соответствии с методом зеркальных отображений это энергия взаимодействия двух разноименных точечных зарядов.

При бесконечном удалении заряда q ϕ_q  = 0. Можно ли считать работу по удалению заряда от плоскости по формуле A = q(ϕ ϕ_{q r} − _{q ∞})^{= −}_8πε^q0_r ?

Нет, нельзя! Эта формула справедлива для движения заряда q в электростатическом поле, когда остальные заряды покоятся. Но в нашем случае при удалении заряда q начнет перераспределяться индуцированный заряд. Это эквивалентно тому, что симметрично удаляется «зеркальный» заряд −q. И т.к. сила взаимодействия между зарядом q и индуцированным на плоскости зарядом σ_ин эквивалентна силе взаимодействия зарядов q и

−q; работа этой силы A = ∫∞r Fdr = − 4πεq2 0 ∫∞r ( )2drr 2 = + 4πεq02 ⋅4 ⋅1r ∞r = A = −16πεq2 0r .

Ответ: qR =−q_1− R2r+r2 , ϕq =−8πεq0r , Wвз =−8πεq0r , A = −16πεq2 0r .

3. Тонкое проводящее кольцо радиусом R , имеющее заряд q, расположено параллельно проводящей безграничной плоскости на расстоянии l от нее. Найти поверхностную плотность заряда в точке плоскости, расположенной симметрично относительно кольца и потенциал электростатического поля в центре кольца.