Электрическое поле в веществе. Основные определения и формулы. Проводник в электрическом поле. Силы, действующие на поверхность проводника, страница 5

                                                                         зарядом dq = ρdV = ρ₀ ^_ _R^{r }_ⁿ 4πr dr²                                                                                                                                                                 .

Тогда заряд внутри сферы r равен

q = ∫r 4πρ0 rn+2dr = 4πρ0 rn+3 при r < R ,

0 Rn n+3 n+3 q R при r > R .

4πρ0 rn 3 при <Rr ρ ε

Тогда 4πr E2 = εq0 = 4πρ0R nn0 R++33 при >Rr⇒ E = εε00 ((ρnn00++33)) rRrRn23+n1припри >Rr <Rr    .

                                             ε0                           n +3

Тогда энергия поля

R ε

Wвнутри              0Eвнут2                 r dr ε ρ π2 ⋅4            R r n+ r dr            2πρ2               R2n+5

шара

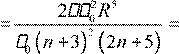 Wвнутри шара

∞

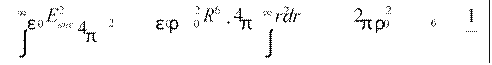Wшаравне = R 2   r dr = 2 ε02 (n+3) R r4         =  0          2 R − 2  R =

                                                                                                ε (n +3)                

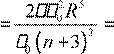W_вне шара

Приравнивая W_вне =W_внутри , получаем 2n +5 =1 или n = −2.

При n = 0 , когда заряд по шару распределен равномерно ^{Wвнутри} ₌ ¹,

                                                                                                                                                                       W_вне 5

независимо от радиуса шара в нем локализовано только 6,7% энергии поля. Ответ: n = −2.

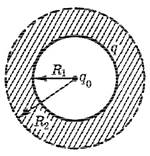
11. Имеется сферическая оболочка, заряженная равномерно зарядом q. В центре ее расположен точечный заряд q₀ . Найти работу электрических сил этой системы при расширении оболочки  увеличение ее радиуса от R₁ до R₂ .

Решение:

Работа электрических сил равна убыли электрической энергии системы:

A =W₁ −W₂ .

                                              Чтобы найти разность          W₁ −W₂ , заметим, что при расширении оболочки электрическое поле, а следовательно, и локализованная в нем энергия изменились только в заштрихованном сферическом слое. Значит,

W₁ −W₂ = ^RR^∫1^{2 ε}₂⁰ (E₁² − E₂² )4πr dr² , где E₁ и E₂  напряженность поля (в заштрихованном слое на расстоянии r от центра системы) до и после расширения оболочки. С помощью теоремы Гаусса находим

E1 = 1 0 q +2q0 , E2 = 4πε1 0 qr20 .

4πε r

В результате интегрирования получим A = ^{q q(} ₄⁰_πε^{+ q}0 ^2)_{ R}¹1 − _R¹2 _^.

Если эту работу искать через потенциал как A = q(ϕ ϕ₁ − ₂ ), где ϕ  потенциал, создаваемый зарядом q₀ в месте нахождения заряда q, ответ будет другим  неверным. Связано это с тем, что при таком подходе не учитывается та дополнительная работа, которую совершают электрические силы при изменении конфигурации заряда q на расширяющейся оболочке.

Ответ: A = q q( 40πε+ q0 2) R11 − R12 .

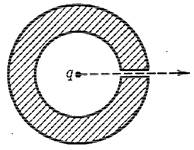12. Точечный заряд q находится в центре сферического незаряженного проводящего слоя, внутренний и наружный радиусы которого равны соответственно a и b . Какую работу произведут

электрические силы в данной системе, если  заряд q переместить на очень большое расстояние от сферического слоя?

Решение:

Будем исходить из того, что работа электрических сил равна убыли электрической энергии системы. Последняя же, локализована в самом поле. Поэтому вопрос сводится к выяснению, как изменится само поле в результате этого процесса.

Поле вокруг заряда q изменится только в сферическом слое с внутренним и наружным радиусами a и b . В начальном положении заряда поля здесь не было, а в конечном положении поле в этом слое есть (ведь сам сферический проводящий слой будет находиться далеко от заряда q).

2

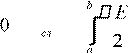Следовательно, искомая работа A =   −W = −    ⁰          dV .

Имея в виду, что E = _4πε^q0_r2 и dV = 4πr dr²                           , получим после интегрирования

A = q2 a −b < 0. 8πε₀ ab

^q2 ^{a −b} < 0.

Ответ: A =

8πε₀ ab