1) Без учета деформаций уравнение теплопроводности записывается в виде
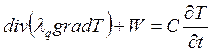 .
.
Если источники отсутствуют, то уравнение теплопроводности переходит в уравнение
1. 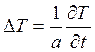 . 2.
. 2.
![]() .
.
2) В выражении ![]() величины
Sijkl называются:
величины
Sijkl называются:
1. Модулями упругости.
2. Модулями упругой податливости.
3. Температурными напряжениями.
3) В выражении ![]() величины
αij называются:
величины
αij называются:
1. Коэффициентами теплопроводности.
2. Коэффициентами линейного расширения.
3. Коэффициентами температуропроводности.
4) Величины ![]() называются
компонентами
называются
компонентами
1. Смещений в точке.
2. Напряжений в точке.
3. Деформаций в точке.
5) В законе Дюамеля – Неймана σij=λijklεkl-βijθ величины βij называются
1. Температурными напряжениями.
2. Коэффициентами теплопроводности.
3. Коэффициентами линейного расширения.
6). В линейной теории упругости предполагается, что перемещения и их производные
1. Малые величины.
2. Конечные величины.
3. Большие величины.
7) В общем случае для постановки задач термоупругости требуется определить
1. 14 функций координат xk и времени t, k=1,2,3.
2. 18 функций координат xk и времени t, k=1,2,3.
3. 16 функций координат xk и времени t, k=1,2,3.
8). В произвольной ортогональной криволинейной системе координат (a,b,g) компонента тензора малых деформаций записана в виде:
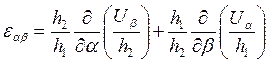 , где h1, h2, h3-
коэффициенты Ламе.
, где h1, h2, h3-
коэффициенты Ламе.
Записать эту компоненту в цилиндрических координатах.
1. 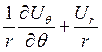 .
2.
.
2. 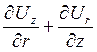 . 3.
. 3. 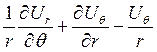 .
.
9) В реальном теле поля перемещений и температуры оказываются взаимосвязанными. Это происходит из – за
1. Подвода тепла от внешних источников.
2. Вследствие процесса деформирования.
3. Не только из – за подвода тепла от внешних источников, но и в следствие процесса деформирования.
10.) В четырёхиндексном
обозначении упругий модуль записан в виде ![]() .
Написать его в двухиндексном обозначении:
.
Написать его в двухиндексном обозначении:
1. ![]() .
2.
.
2. ![]() . 3.
. 3. ![]()
11). Выражение напряжения через смещение и температуру
sij=lUk,kdij+m(Ui,j+Uj,i)-(3l+2m)a(T-T0) dij
записано для
1. Изотропного тела. 2. Анизотропного тела.
12.) Выражение
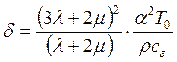 есть
есть
1. Коэффициент теплопроводности.
2. Коэффициент (параметр) связанности.
3. Символ Кронекера.
13) Выражение ![]() называется
называется
1. Уравнением равновесия.
2. Законом Гука.
3. Обобщенным законом Гука.
14) Выражение ![]() σij=λijkl εkm называется
σij=λijkl εkm называется
1. Уравнением равновесия.
2. Законом Гука.
3. Обобщенным законом Гука
15). Главные коэффициенты теплопроводности кварца имеют следующие значения (в единицах системы СИ вт/(м*град)): к1=к2=6.5; к3=11.3. Написать уравнение характеристической поверхности тензора удельной теплопроводности для этого кристалла:
1. х12+2х22+3х32=1. 2. 6.5(х12+х22)+11. 3х32=1.
16) Граничное тепловое условие записано в виде:
![]() .
.
Это есть:
1. Распределение температуры на границе двух тел.
2. Плотность теплового потока через поверхность тел на границе.
3. Теплообмен излучением между поверхностями.
17) Граничное тепловое условие записано в виде
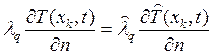 .
.
Это есть:
1. Распределение температуры на границе двух тел.
2. Плотность теплового потока через поверхность тел на границе.
3. Теплообмен излучением между поверхностями.
18)Граничное тепловое условие имеет вид
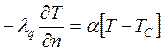 , где a -
коэффициент теплоотдачи, Ts - температура среды.
, где a -
коэффициент теплоотдачи, Ts - температура среды.
Это есть:
1. Распределение температуры на границе тела и среды.
2. Температура окружающей среды Ts и закон конвективного теплообмена между поверхностью тела и средой.
19)Граничные условия записаны в виде
Ux=0, Uy=0, Ut=0.
Это есть:
1. Свободная граница.
2. Граница упругого тела с абсолютно жестким телом.
3. Граница с идеальной жидкостью.
20)Граничные условия записаны в виде
sxx=0, sxy=0, sxz=0.
Это есть:
1. Свободная граница.
2. Граница упругого тела с абсолютно жестким телом.
3. Граница с идеальной жидкостью.
21)Граничные условия записаны в виде
sxx=-p, sxy=0, sxz=0, Un= U/n.
где n – ось, совпадающая с нормалью к границе.
Это есть:
1. Свободная граница.
2. Граница упругого тела с абсолютно жестким телом.
3. Граница с идеальной жидкостью.
22.) Диагональные элементы тензора напряжений
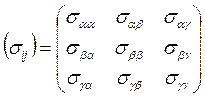 определяют:
определяют:
1. Касательные напряжения.
2. Нормальные напряжения.
23)Дано уравнение: 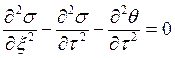 . Написать это уравнение,
преобразованное по Лапласу.
. Написать это уравнение,
преобразованное по Лапласу.
1. 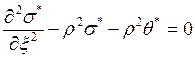 .
.
2. 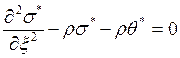
24). Для какого тела записаны уравнения обобщённого закона Гука?
sxx=l11exx+l12eyy+l13ezz, syz=l44eyz,
syy=l12exx+l11eyy+l13ezz, szx=l44ezx,
szz=l13(exx+eyy)+l33ezz, sxy=2(l11-l12)exy.
1. Изотропного. 2. Ортотропного. 3. Трансверсально-изотропного.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.