Математическое описание узлов привода главного движения и методики их расчетов. Система автоматизированного проектирования привода главного движения

2. Математическое описание узлов привода главного движения и методики их расчетов

Рассмотрим математические описания и методики расчетов узлов привода главного движения:

- чисел зубьев групповых передач;

- прямозубой цилиндрической передачи на прочность;

- клиноременной передачи;

- опорных реакций, статической и динамической грузоподъемности подшипников и изгибающих моментов вала;

- сечений сплошного вала на статическую прочность и выносливость;

- шпинделя на изгибную жесткость.

2.1. Расчет чисел зубьев групповых передач

Расчет чисел зубьев передач можно производить по следующей схеме. Пусть в группе заданы следующие значения передаточных отношений:

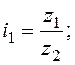
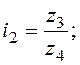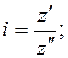             ...       ;        ...    ,                                (2.1)

где z' - число зубьев ведущей шестерни; z'' - число зубьев ведомой шестерни.

В большинстве случаев, чтобы упростить изготовление станка модули всех зубчатых передач одной и той же группы делают одинаковыми, следовательно, должно быть

,                                  (2.2) 

где  - сумма зубьев.

Используя (2.1) и (2.2), выразим z' и z'' через i и :

,                                                                      (2.3)

 ,

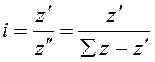откуда 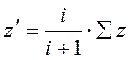                                     .                                                          (2.4)

Таким образом, зная передаточные отношения i и сумму зубьев , по формулам (2.3) и (2.4) можно рассчитать числа зубьев в передачах группы. Поскольку числа зубьев - целые числа, то значение z', полученное по формуле (2.4), необходимо округлять до целого и в общем случае фактическое передаточное отношение i_ф будет отличаться от заданного i:

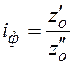,                                                         (2.5)

где 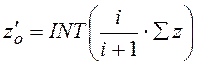                                                               ,                                       (2.6)

.                                                (2.7)

Здесь INT() - операция округления до целого; z'_о и z''_о - округленные значения чисел зубьев передачи.

Из (2.5) - (2.7) видно, что, варьируя , можно получать различные i_ф. Таким образом, перебирая возможные значения , можно найти оптимальную сумму зубьев и соответственно числа зубьев передачи z'_о и z''_о, при которых разность  будет минимальной. Поскольку в общем случае передаточные отношения в группе зубчатых передач различны по абсолютной величине, то в качестве критерия минимизации следует принять относительную погрешность передаточного отношения:

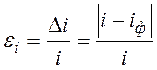.                                           (2.8)

В расчете необходимо учитывать следующие ограничения:

- число зубьев некорригированных колес ;

- сумма зубьев.

Учитывая вышеизложенное, можно составить следующую блок-схему алгоритма нахождения чисел зубьев (рис. 2.1).

Исходные данные:

n - количество передач в группе;

i[n] - массив передаточных отношений;

 - минимальная сумма зубьев;

 - максимальная сумма зубьев.

В цикле перебираются значения суммы зубьев от  до  . Для каждого значения  выполняется вложенный цикл, в котором для j-й передачи производятся следующие действия. По формулам (2.6) и (2.7) вычисляются числа зубьев z'_о[j] и z''_о[j]. Если число зубьев ведущей или ведомой шестерни меньше допустимого, то осуществляется выход из вложенного цикла и переход к рассмотрению следующего значения . При допустимых значениях z'_о[j] и z''_о[j] вычисляются фактическое передаточное отношение i_ф[j] и относительная погрешность  по формулам (2.5) и (2.8) соответственно. Далее переменной  присваивается наибольшее значение .

На выходе из вложенного цикла  содержит наибольшее значение относительной погрешности для передаточных отношений в группе при текущем . Далее  сравнивается с  - максимальным текущим значением относительной погрешности.  Если , то числа зубьев передач сохраняются в соответствующих массивах z'[n] и z''[n], а  присваивается значение . Далее выполняется цикл с новым значением .

Таким образом, в конце программы в массивах z'[n] и z''[n] будут содержаться оптимальные значения чисел зубьев передач.

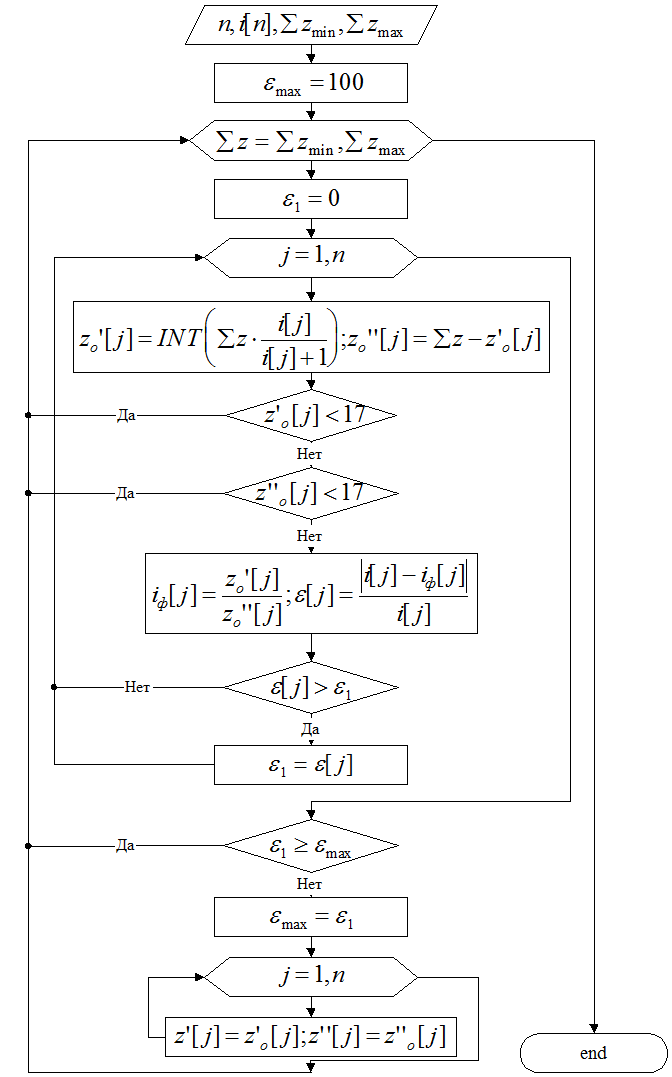
Рис. 2.1. Алгоритм расчета чисел зубьев групповых передач

2.2. Расчет прямозубой цилиндрической передачи на прочность

Предлагаемая методика позволяет производить расчет силовых зубчатых