Уравнение теплопроводности. Выражение напряжения через смещение и температуру. Уравнением равновесия, страница 2

25). Для какого тела записаны уравнения обобщённого закона Гука?

s_xx=l₁₁e_xx+l₁₂e_yy+l₁₃e_zz, s_yz=l₄₄e_yz,

s_yy=l₁₂e_xx+l₂₂e_yy+l₂₃e_zz, s_zx=l₅₅e_zx,

s_zz=l₁₃e_xx+l₂₃e_yy+l₃₃e_zz, s_xy=l₆₆e_xy.

1. Изотропного. 2. Ортотропного. 3. Трансверсально-изотропного.

26) Для какого тела записаны уравнения обобщённого закона Гука?

s_xx=(l+2m)e_xx+l(e_yy+e_zz), s_xy=me_xy,

s_yy=(l+2m)e_yy+l(e_xx+e_zz), s_xz=me_xz,

s_zz=(l+2m)e_zz+l(e_xx+e_yy), s_yz=me_yz.

1. Изотропного. 2. Ортотропного. 3. Трансверсально-изотропного.

27) Для постановки задачи термоупругости в замкнутой форме необходимо задать:

1. Начальные условия.

2. Граничные условия.

3. Начальные и граничные условия.

28.) Для получения результатов по любой физической или технической проблеме необходимы:

1. Постановка задачи, которая включает выбор модели, адекватной данной задаче, и определение исходных параметров этой модели.

2. Математическое решение модели.

3. Проверка полученных результатов.

Какой из этих этапов допускает строгое математическое (логическое) решение?

1. Первый. 2. Второй. 3. Третий.

29). Если в уравнениях ,  положить , то мы получим линеаризованное уравнение

1. Вязкой несжимаемой жидкости

2. Идеальной сжимаемой жидкости.

3. Ламе.

30.) Если , то

1. Поверхности тела теплоизолированы.

2. Это есть условие свободного (конвективного) теплообмена на поверхности S с окружающей средой.

3. Распределение температуры по поверхности тела.

31) Если существует функция энергии деформации, то анизотропное тело имеет матрицу упругих констант из

1. 36 независимых постоянных

2. 21 независимых постоянных

3. 12 независимых постоянных

32). Закон Фурье для термоупругой анизотропной среды имееет вид:

1. .        2. .

33). Закон Гука  пригоден

1. В любой системе координат.

2. В любых ортогональных криволинейных координатах.

3. В прямоугольной системе координат.

34) Закон Дюамеля – Неймана соответствует:

1. Закону сохранения энергии.

2. Закону теплопроводности Фурье.

3. Закону Гука для изотропной среды.

35).Задачи, в которых рассматриваются гармонические колебания, то есть  относятся

1. К стационарным динамическим задачам.

2. К нестационарным динамическим задачам

36) Какая система характеризуется девятью постоянными λ_ijkl ?

1. Гексагональная.

2. Ортогональная

37). Как запишутся деформации через смещения, если имеем случай осевой симметрии, когда имеет место только радиальное смещение U_r?

1.

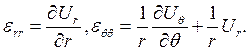
2.

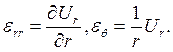
38) Какие компоненты определяются соотношениями

:

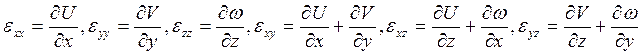1. Напряжений.

2. Деформаций.

3. Смещений.

39). Какому температурному полю отвечает уравнение Лапласа ?

1. Нестационарному. 2. Стационарному.

40). Какой вид имеет решение уравнения Лапласа 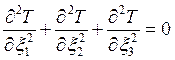 в случае, когда единственный источник тепла лежит в начале координат?

1. 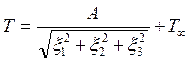. 2.

41). Когда напряжения считаются отрицательными?

1. При растяжении. 2. При сжатии.

42) Коэффициент С_ε называется:

1. Удельной теплоемкостью при постоянном давлении.

2. Удельной теплоемкостью при постоянном тензоре напряжений.

Удельной теплоемкостью при постоянной деформации

43). Конструкционные материалы являются анизотропными, если

1. Их свойства, измеренные в разных направлениях, совпадают.

2. Их свойства, измеренные в разных направлениях, не совпадают.

44) К решению системы уравнений

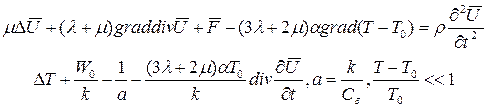
сводится

1. Связная задача термоупругости.

2. Несвязная задача термоупругости.

45). Матрица

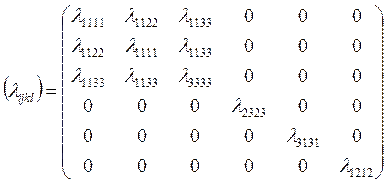
есть матрица модулей для

1. Ортотропной системы. 2. Трансверсально-изотропной системы.

Записать эту матрицу в двухиндексном обозначении.

46) . Матрица

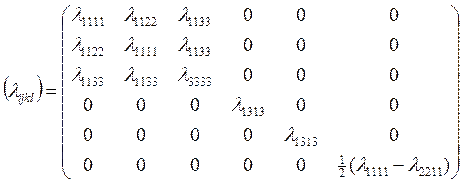
есть матрица модулей для

1. Ортотропной системы. 2. Трансверсально-изотропной системы.

Записать эту матрицу в двухиндексном обозначении.

47). Матрица

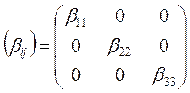 имеет место для

1. Общего случая анизотропии.

2. Ортотропной системы.

3. Трансверсально-изотропной системы.

48) Матрица тензора β_ij

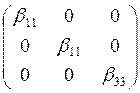
соответствует кристаллам

1. Моноклинной системы.

2. Гексагональной системы.

3. Ромбического типа кристаллов.

49) Матрицу упругих констант:

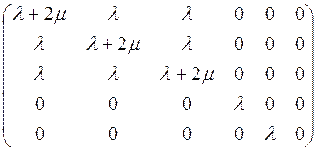
имеет:

1.Термоупругое тело.

2.Анизотропное тело.

3.Изотропное тело.

50) На границе раздела двух термоупругих сред задаются:

1. Механические условия.

2. Тепловые граничные  условия.

3. Механические и тепловые граничные условия.

51) Напряжением называется

1. Интенсивность внутренних сил.

2. Интенсивность внешних сил.

3. Интенсивность деформаций.

52). Написать общее решение уравнения

.

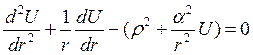1. U(r,p)=A(p)H_a⁽¹⁾(pr)+ B(p)H_a⁽²⁾(pr).

2. U(r,p)=A(p)K_a(pr)+ B(p)I_a(pr).

3. U(r,p)=A(p)K_a(pr).