Уравнение теплопроводности. Выражение напряжения через смещение и температуру. Уравнением равновесия, страница 4

2.Тремя взаимно перпендикулярными плоскостями симметрии.

3.Бесчисленным множеством плоскостей симметрии.

76). Соотношения  есть

1. Закон Гука для идеально упругого анизотропного тела.

2. Соотношение Дюамеля-Неймана.

77). Среда называется термоупругой средой:

1. Если в ней невозможен обратимый упругий процесс и обратимый тепловой процесс.

2. Если в ней возможен обратимый упругий процесс и необратимый тепловой процесс.

78). Теплопроводностью называется:

1. Перенос тепла в твёрдом теле от мест с более высокой температурой к местам с более низкой температурой.

2. Перенос тепла в твёрдом теле от мест с более низкой температурой к местам с более высокой температурой.

79) Тензор деформации e определяется линейной зависимостью вида e_ij=1/2(U_i,j=U_j,i).Удовлетворяют ли его компоненты условию симметрии?

1. Да.            2. Нет.

80). Тензоры, описывающие свойства кристаллов, называются

1. Полевыми. 2. Материальными.

81). Тензоры напряжений и деформации описывают соответственно внешнее напряжение на  кристалл и реакцию кристалла на это воздействие. Они называются

1. Полевыми. 2. Материальными.

82) Тензор деформаций Грина имеет вид:

.

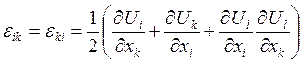Если компоненты тензора деформаций малы, то какой вид имеет написанное выше выражение?

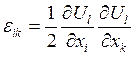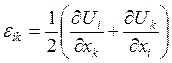1. .          2. .          3. .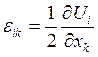

83) Уравнение  называется

1. Уравнением Навье – Коши.

2. Уравнением Навье – Стокса.

3. Уравнением Ламе.

84). Уравнение движения упругого тела в напряжениях в цилиндрических координатах в случае радиальной симметрии имеет вид:

.

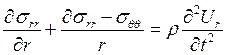Это уравнение справедливо

1. Для идеально упругого изотропного тела.

2. Для термоупругого тела.

3. Для анизотропного тела.

4. Для любого упругого тела.

85). Уравнение характеристической поверхности тензора k_ij записывается в виде k_ijx_ix_j=1, а после приведения к главным осям - в виде:

1. k₁₁х₁²+k₂₂х₂²+k₃₃х₃²=1.           2. K₁х₁²+k₂х₂²+k₃х₃²=1.

86). Уравнение движения в полярных координатах, полюс которых совпадает с центром кругового отверстия, имеет вид:

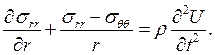
Подставляя сюда напряжения по формулам:

s_rr=l₁₁e_rr+l₁₂e_qq, s_qq=l₁₂e_rr+l₂₂e_qq

и выражая деформацию через смещение, приходим к уравнению:

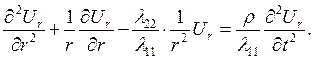
Как решается последнее уравнение?

1. Методом разделения переменных.

2. Преобразованием Лапласа по времени.

87). Уравнения  справедливы

1. В декартовой системе координат.

2. В цилиндрической системе координат.

3. В любой системе координат.

88). Упругие модули удовлетворяют соотношениям . Благодаря этим условиям число этих независимых модулей будет

1. Не более 6. 2. Не более 13. 3. Не более 21.

89). Уравнение теплопроводности 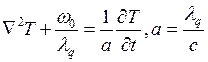 записано

1. С учётом деформаций. 2. Без учёта деформаций.

90). Уравнение s_ij,j+C_i=0 есть

1. Уравнение движения упругого тела.

2. Уравнение равновесия.

91). Уравнение s_ij,j+F_i= справедливо

1. Для упругих сред.

2. Для любых сред и процессов.

92) Уравнения  являются:

1. Уравнениями Ламе.

2. Соотношениями Дюамеля – Неймана.

3. Определяющими уравнениями термоупругости.

93). Уравнение характеристической поверхности единичного тензора d_ijx_ix_j=1. Показать, что это есть

1. Трёхосный эллипсоид. 2. Эллипсоид вращения. 3. Сфера единичного радиуса.

94) Уравнение  есть:

1. Уравнение теплопроводности.

2. Обобщенное уравнение теплопроводности.

3. Уравнение притока тепла связанной термоупругости.

95). Уравнения , в случае гармонических колебаний являются

1. Гиперболической системой уравнений.

2. Параболической системой уравнений.

3. Эллиптической системой уравнений.

96). Упругие свойства трансверсально-изотропной среды описываются:

1. Пятью модулями упругости. 2. Тринадцатью модулями упругости. 3. 21 модулем упругости.

97) Упругое тело, обладающее гексагональной симметрией (трансверсально – изотропная среда), определяется

1. Двумя независимыми коэффициентами.

2. Пятью независимыми коэффициентами.

3. Девятью независимыми коэффициентами.

98) Эффект связности поля деформаций и температурного поля мало влияет на термические возмущения и распределение тепловых напряжений:

1. В металлических телах.

2. В материалах с большим параметром связности.

99)

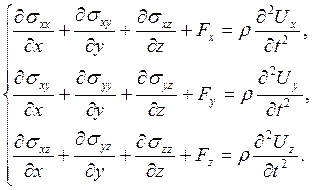
Это запись в декартовой системе координат:

1. Уравнений движения сплошной среды.

2. Дифференциальные уравнения равновесия.

100)      

Здесь записаны:

1. Граничные условия на границе области D¯.

2. Начальные условия, необходимые для однозначного решения задачи связанной термоупругости.

101) .

Это есть:

1. Соотношения Дюамеля – Неймана.

2. Уравнение Навье – Стокса.

3. Обобщенный закон Гука.