53). Найти уравнения изотермических поверхностей, если тепло в кристалле кварца (к1=к2=6.5; к3=11.3) распространяется от точечного источника.
1. 6.5(х12+х22)+11.3х32=С. 2. х12/6.5+х22/6.5+х32/11.5=С.
54). Написать общее решение
уравнения ![]() .
.
1. y(x)=AnJn(x)+BnNn(x)=CnHn(1)(x)+ DnHn(2)(x).
2. y(x)=AnKn(x)+BnJn(x).
55.) Напряжения определяются по формулам:
srr=l11err+l12eqq, sqq=l12err+l22eqq.
Для какого материала записаны эти выражения?
1. Для пластины из ортотропного материала с цилиндрической анизотропией.
2. Для пластины из трансверсально-изотропного материала с цилиндрической анизотропией.
56). Ниже приведены модуль задачи о распространении упругого импульса, обусловленного осесимметричным давлением, приложенным к контуру кругового отверстия в безграничной тонкой пластине, материал которой цилиндрически анизотропен:
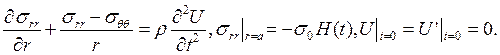
Какие условия нужно добавить для однозначного решения модели?
1. В центре отверстия возмущения должны быть ограниченными.
2. На бесконечности возмущения должны затухать.
57). Ниже приведены модуль задачи о распространении упругого импульса, обусловленного осесимметричным давлением, приложенным к контуру кругового отверстия в безграничной тонкой пластине, материал которой цилиндрически анизотропен:
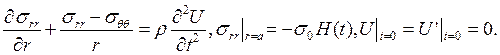
В граничном условии H(t) есть
1. Функция Ханкеля первого рода.
2. Единичная функция Хевисайда.
3. Гармоническая функция.
58) Обобщенное уравнение теплопроводности имеет вид:
![]()
в отсутствии источников тепла. Какой член этого уравнения определяет сопряжение поля температуры и поля деформации.
1. Первый.
2. Второй.
3. Третий.
59) Образуют ли полную систему уравнений термоупругости анизотропных тел уравнения
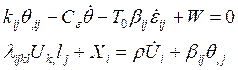
1. Да.
2. Нет.
60) Поверхностными силами называются
1. Силы, распределенные по массе тела.
2. Силы, распределенные по поверхности тела.
3. Силы, отнесенные к единице объема.
61) Показать, что решение уравнения
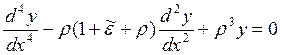
имеет вид:
1) ![]()
2) ![]()
где ![]() - корни
характеристического уравнения
- корни
характеристического уравнения
62)Попарно равны все компоненты смещений обоих тел на границе и одноименные компоненты тензора напряжений:
Ui= U/i ,sxx=s/xx, sxy=s/xy, sxz=s/xz.
Это есть:
1. Граница упругого тела с другим упругим телом.
2. Граница упругого тела с абсолютно жестким телом.
63). Правильно ли записано
соотношение 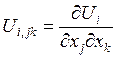 ?
?
1. Да. 2. Нет.
64). Правильно ли записано
соотношение 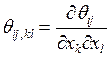
1. Да. 2. Нет.
65) При моделировании стационарных задач на распространение волн в упругом теле необходимо решить
1. Одно уравнение Гельмгольца.
2. Два уравнение Гельмгольца.
3. Три уравнение Гельмгольца.
66). При моделировании стационарных волновых процессов в термоупругом теле необходимо решить:
1. Два уравнения Гельмгольца. 2. Три уравнения Гельмгольца.
67). При решении задачи
распространения цилиндрической волны в анизотропной среде, имеющей круговую
цилиндрическую полость радиуса ![]() , задача
сводится к решению уравнения
, задача
сводится к решению уравнения 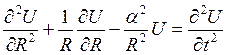 . Какой
вид имеет это уравнение, преобразованное по Лапласу?
. Какой
вид имеет это уравнение, преобразованное по Лапласу?
1.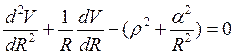 . 2.
. 2. 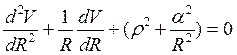
68). При тепловом или силовом воздействии на границу длинной цилиндрической полости в пространстве или на поверхности длинного полого цилиндра тождественно равны нулю все компоненты перемещения кроме одной:
1. Ur, 2. Uq, 3. Uz.
69) Рассмотрим тензор вращения wij с компонентами wij=1/2(Ui,j-Uj,i). Отсюда следует, что wij=-wji, то есть
1. Тензор вращения симметричен.
2. Тензор вращения асимметричен.
70). Связанная теория термоупругости предполагает
1. Отсутствие влияния деформаций на температурное поле.
2. Взаимодействие процессов деформирования и теплопроводности.
71) Система уравнений
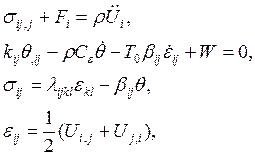
+ начальные и граничные условия есть модель
1. Задачи изотропной упругости.
2. Задачи связанной термоупругости.
3. Задачи связанной анизотропной термоупругости.
72) Система уравнений
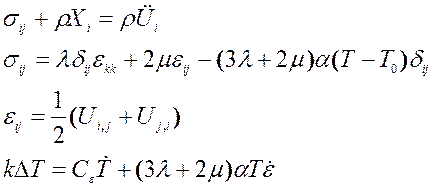 ;
;
есть система уравнений
1. Общей задачи линейной теории упругости.
2. Общей задачи термоупругости для изотропной среды.
3. Общей задачи анизотропной термоупругости.
73) Система уравнений
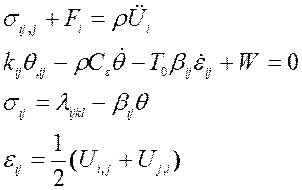
есть система уравнений
1. Общей задачи линейной теории упругости.
2. Общей задачи термоупругости для изотропной среды.
3. Общей задачи анизотропной термоупругости.
74) Система уравнений ![]()
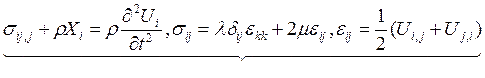
есть система уравнений
1. Общей задачи линейной теории упругости.
2. Общей задачи термоупругости для изотропной среды.
3. Общей задачи анизотропной термоупругости.
75) Среда называется ортотропной, если она обладает:
1.Двумя взаимно перпендикулярными плоскостями симметрии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.