Каждым сечением вырезают один узел (см. рис. 6.3, б), к которому прикладывают внешние силы (если они есть) и продольные усилия Ni в разрезанных стержнях. Для каждого узла плоской фермы (как для материальной точки) можно составить два уравнения статики (уравнения проекций: S X=0; SY=0), а для всей фермы - 2У уравнений (здесь У -число узлов фермы). Наиболее простое решение способ даёт, когда к вырезанному узлу плоской фермы сходится лишь два “неизвестных” стержня. В случае, когда в вырезанном узле сходятся три стержня, решение возможно лишь для частного случая - два стержня находятся на одной прямой ( вначале все силы проектируют на ось, перпендикулярную двум этим неизвестным силам). Поэтому в общем случае при рассмотрении равновесия вырезанного узла неизвестными должы оставаться лишь два усилия – остальные должны быть определены предварительно при вырезании предыдущих узлов.
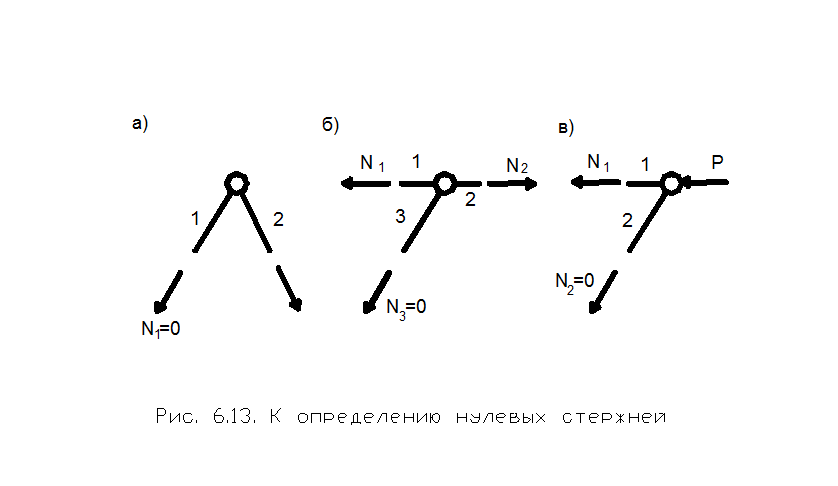
С целью упрощения расчётов следует пользоваться признаками, позволяющими установить нулевые (неработающие) стержни в плоской ферме: а) в ненагруженном двухстержневом узле оба стержня являются нулевыми, если их оси не лежат на одной прямой (рис. 6.8,а); б) если в ненагруженном трёхстержневом узле оси двух стержней лежат на одной прямой, то третий - нулевой (рис. 6.8, б); в) то же, если вместо второго стержня прложена сила Р (рис. 6.8, в).
6.5. Главная балка мостового крана
Расчет главной балка мостового крана подробно рассмотрен в работе [6].
6.6. Тяговая рама скрепера
Расчётная схема показана на рис. 6. . Реактивные силы в упряжных шарнирах рамы представлены в виде проекций на оси координат x, y, z.
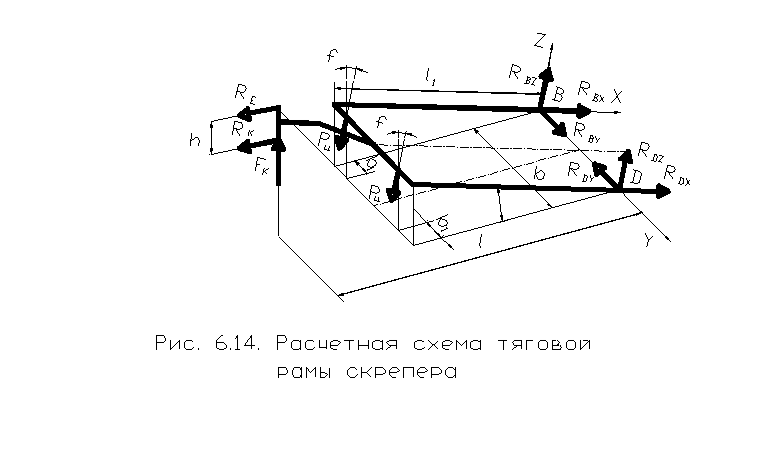
Составляющие реакций в упряжных шарнирах, перпендикулярные плоскости рамы, RВz и RDz могут быть найдены из уравнения проекций сил на ось z:
RBz = RDz = ½[(RE + RK)sing -FK cosg ] + PЦ cosd .
Составляющие реакций шарниров в плоскости рамы (RBx , RDx, RBy, RDy) определяются от действия сил, приведённых в плоскость рамы:
реакция хобота рамы (Х=0)
R’ = (RE + RK )cosg + FK sing ;
силы на штоке гидроцилиндра подъёма ковша
PЦ’ = PЦ sind .
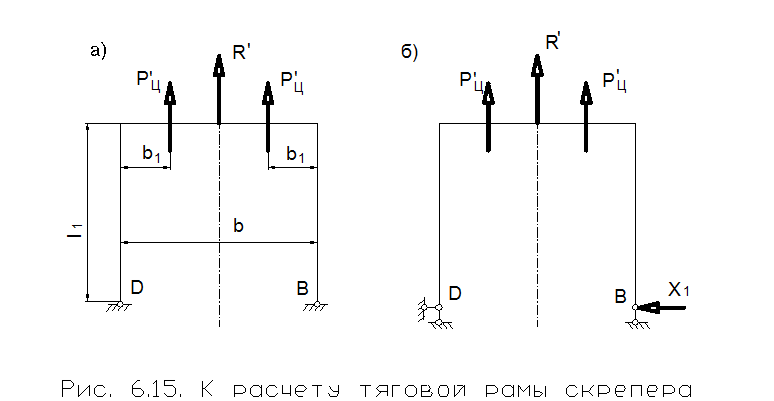
Расчётная схема (рис. 6.15, а) - один раз статически неопределима. Искомые неизвестные могут быть найдены по методу сил. Основная система (рис. 6.15, б) может быть получена заменой горизонтального опорного стержня неизвестным усилием X1.
Поперечная балка рамы находится в сложно напряжённом состоянии под действием крутящего момента (рис. 6.14):
Мкр = RDz l ;
a также изгибающих моментов в плоскостях xy и xz:
Mz = RDy l1 + RDx b/2 – PЦ sind(b/2-b1);
Mх = RDz b/2-PЦ cosd (b/2-b1).
Упряжные тяги рассчитывают на изгиб в плоскостях zx и xy с учётом продольной силы RDx и RBx.
Хобот рамы рассчитывается как кривой брус на изгиб от действия силы RE , RK и FK.
Расчёт тяговой рамы и её элементов удобно вести с использованием ЭВМ по методу конечных элементов.
6.7. Расчет стрелы экскаватора
Расчетная схема приведена на рис. 6.17, а, эпюры усилий на рис. 6.17, б, в. Действующие на рабочее оборудование нагрузки, за исключением Рb, расположены в вертикальной плоскости симметрии. При этом в стреле возникают не только изгибающие, но и крутящие моменты.
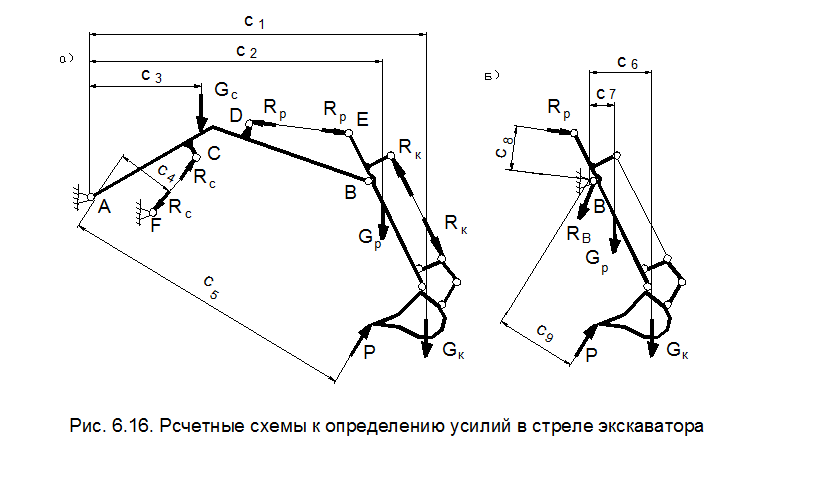
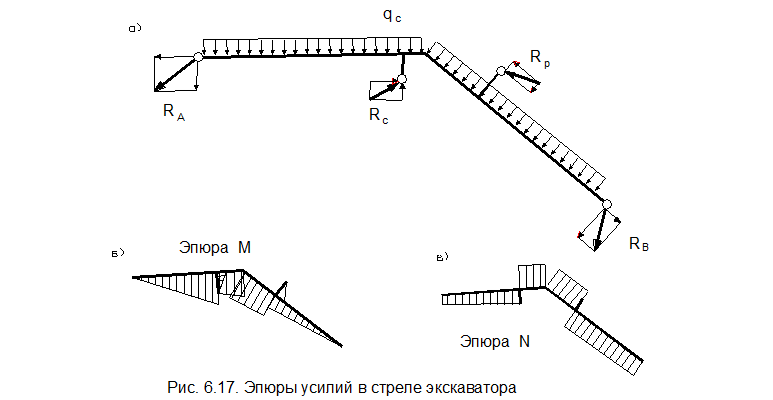
Для определения действующих в поперечных сечениях стрелы усилий необходимо определить реакции в шарнирах A и В, а так же в стержнях DE и FC (гидроцилиндры) (рис. 6.16 , а).
Реактивную силу в гидроцилиндрах стрелы Rc можно найти из условия равновесия всего рабочего оборудования:
Rс = ( c5 Р + c3 Gc + c2 Gp + c1 Gk ) / c4 , где Gc, Gр, Gк – силы тяжести соответственно стрелы, рукояти, ковша (см. п. 3).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.