Механика \ Прикладная механика

Определение усилий. Методы расчета. Расчет статически неопределимых систем. Формулы для расчета интегралов, страница 6

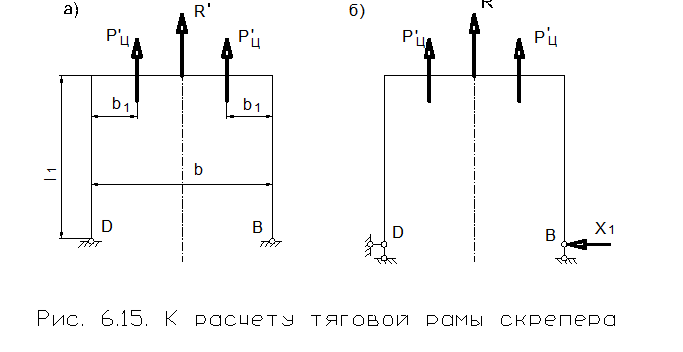
Расчётное усилие  сжатия  в нижнем поясе у опорного шарнира (рис. 6.7, б)

Nп = Rв / 2cos  a2  + Rг / cos  a2 .

Расчётные усилия в поясах в средней части стрелы, где  a2 =0, определяются от продольной силы N,  момента от горизонтальных  нагрузок  Mг, момента от вертикальных нагрузок M и от эксцентриситета Me:

Mе = N e, где e = 0,33 h  -  расстояние  от центра тяжести сечения стрелы до нижней грани.

Тогда усилие в нижнем поясе (с учётом догрузки от Mе)

Nп = N/3 + Mг / b – M / 2h + Mе / 2h, где h - высота треугольника  (стрелы).

Усилие в верхнем поясе (с учётом разгрузки от Ме)

Nп = N/3 + (M- Mе)/h.

6.2.4. Усилия в элементах соединительных решеток стрелы

Усилия в элементах соединительной решетки определяются по зависимостям (6.14) и (6.55) от реальной Q (см. эпюры Q, рис. 6.1) или от условной поперечной силы Qусл. Предполагается, что Qусл возникает при условии продольного изгиба стрелы. Ее определяют в зависимости от площади поперечного сечения стрелы (сумма площадей поясов) и механических характеристик материала (см. табл. 6.2)

Таблица 6.2 - Условная поперечная сила Qусл

sт, МПа

240

250-310

330-400

410-450

460-600

610-700

Qусл, кН

0,2 Ас

0,3 Ас

0,4 Ас

0,5Ас

0,6 Ас

0,7 Ас

Примечание. sт – предел текучести стали; Ас – площадь поперечного сечения стрелы, см2.

Поперечное усилие, приходящиеся на решетку одной плоской фермы, равно

Qр = Qmax / np cosb , где Qmax –большее из усилий  в сечении стрелы: Q, взятое по эпюрам, или Qусл.

np – количество плоских ферм (решеток), воспринимающих Q,

b - угол между плоскими фермами (решетками), воспринимающими Q.

6.3. Ферма козлового крана

В качестве расчетного рассмотрим состояние, при котором на кран действуют максимальные нагрузки рабочего состояния: кран с грузом находится в движении (состояние II, б).

В отличии от стрел, в фермах козловых кранов возникают усилия, обусловленные их изгибом в вертикальной и горизонтальной плоскостях, М и Q. Продольное усилие N в поперечном сечении возникает лишь при действии вдоль фермы ветровой или инерционной (при разгоне или торможении грузовой тележки) нагрузок. Эти нагрузки невелики, поэтому в работе не рассматриваются. Также, как и в балочных стрелах, нагрузка от веса груза является подвижной.

Расчет ферм аналогичен расчету стрел (см. п. 6.2.1).

6.3.1. Расчет фермы  на нагрузки в вертикальной плоскости

При построении эпюр M и Q в плоскости подвеса груза  за расчетную схему  может быть принята многоопорная балка. Особенностью данной схемы является то, что она один раз статически неопределима при наличии одной жесткой опоры, и дважды - при двух жестких опорах. С целью упрощения расчетов на практике принято опорные реакции RA и RB определять на уровне головок рельсов, а затем опорную реакцию представлять в виде двух составляющих R’A = RA/2 (R’B = Rb/2), приложенных в точках примыкания жесткой опоры к опорному строению (рис. 6.9, а). Чтобы система при этом оставалась геометрически неизменяемой введем “нулевую”  горизонтальную связь. Примеры эпюр изгибающих моментов от собственного веса Мq и подвижной нагрузки МF, расположенной на правой опоре, показаны  на рис. 6.9, б, в, а эпюры  поперечных сил от собственного веса фермы qф и от подвижной нагрузки на правой опоре F - на рис.  6.9, г, д.

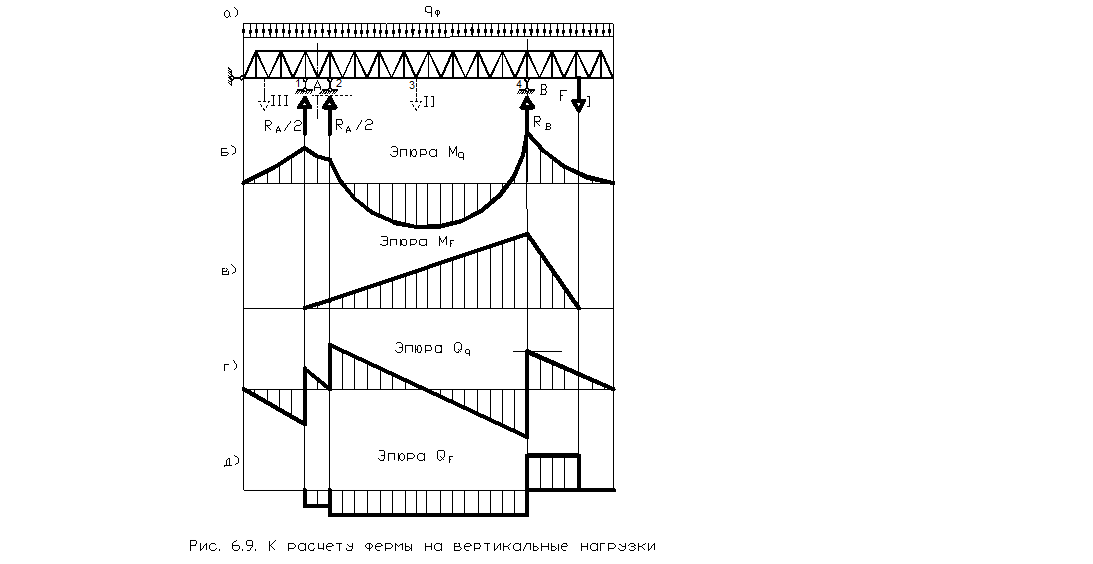
Эпюры изгибающих моментов и поперечных сил строятся для трех положений:

-  тележка посредине пролета;

-  тележка на консоли правой опоры;

-  тележка на консоли левой опоры.

6.3.2. Расчет фермы  на нагрузки в горизонтальной  плоскости

Скачать файл