Определение усилий. Методы расчета. Расчет статически неопределимых систем. Формулы для расчета интегралов, страница 2

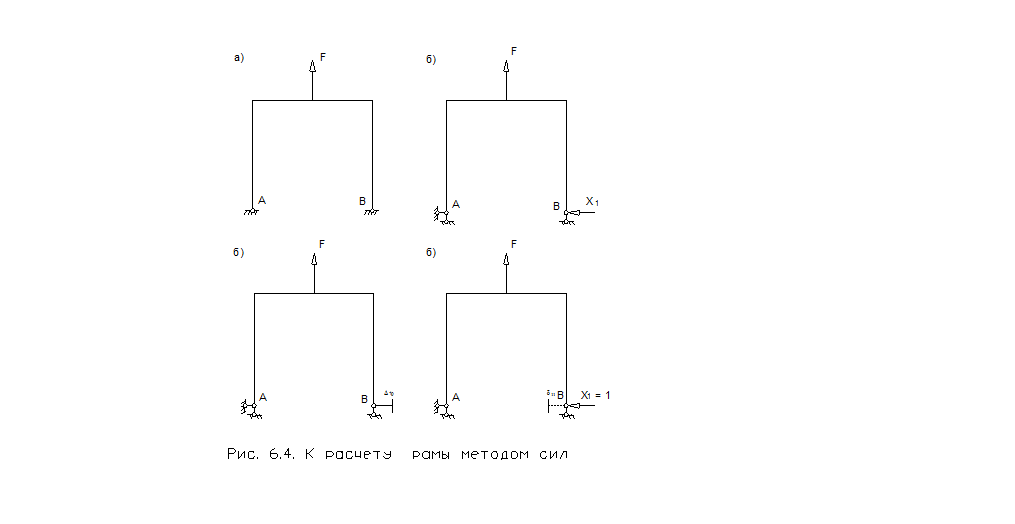
Один раз статически неопределимая система показана на рис. 6.4, а. За основную систему можно принять раму с устраненной горизонтальной связью, вместо которой приложена лишняя неизвестная X₁ (рис. 6.4, б).

При действии лишь внешней нагрузки, правая опора получит перемещение D_1р (рис. 6.4, в). По условиям закрепления заданной системы перемещение отсутствует, поэтому искомое усилие должно возвратить точку в исходное положение. Т.к. значение X₁ неизвестно, то прикладываем усилие X₁ = 1, которое вызовет перемещение d₁₁ (рис. 6.4, г). При действии силы  X₁ в линейно-деформируемой системе перемещение равно d₁₁X₁, тогда условие, выражающее отсутствие перемещения по направлению отброшенной связи, представится так:

d₁₁X₁ + D_1р =0                                                                         (6.2) откуда

 X₁  = - D_1р/d₁₁ ,                                                                      (6.3)

где   D_1P -  перемещение  от внешних сил в направлении действия единичной силы (единичная сила прикладывается в точке приложения неизвестного усилия Х₁ и совпадает с ним по направлению);

d₁₁  - перемещение  от единичной силы в направлении действия единичной силы (X₁ = 1).

После построения эпюр изгибающих моментов от внешней и единичной  нагрузок перемещения могут быть найдены по  формуле Максвелла-Мора:

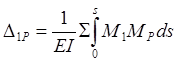 ,                                                           (6.4)

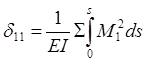                                                 ,                                                               (6.5)

где М_Р и М₁ –  значения изгибающих моментов в расчетном сечении соответственно от внешней нагрузки и единичной силы;

s  - координата рассматриваемого сечения.

Для вычисления интегралов применяется способ Верещагина, заключающийся в “перемножении” эпюр моментов от действия заданной (М_Р) и единичной (М₁) нагрузок (подробнее см. [3], [5], [10]). В целях упрощения расчетов можно использовать расчетные формулы, приведенные в табл. 6.1, если эпюр моментов от действия заданной внешней нагрузки (М_Р) имеет линейный характер (или близкий к линейному).

Таблица 6.1 - Формулы для расчета интегралов

После определения величины Х₁ строят эпюру моментов  от  её  действия, перемножая величину момента от единичной нагрузки на величину Х₁. 

Уравнений типа (6.2) и (6.3) можно составить столько сколько лишних неизвестных в заданной системе.

6.1.2.2. Из-за больших математических трудностей расчета систем с большим количеством лишних связей (особенно с элементами в виде пластин и оболочек) получили широкое развитие численные методы расчета, среди которых наиболее универсальным является метод конечных элементов, применяемый в основном в виде метода перемещений с использованием ЭВМ.

Согласно этому методу, система разбивается на отдельные части – “конечные элементы”, для которых составляются уравнения, описывающие их совместную работу. В стержневых системах конечным элементом является стержень.

В СГУПС имеются профессиональные программы для расчета стержневых систем, плит, оболочек и массивных тел. Расчет стержневых систем может быть выполнен по программам МКЭСС (авт. Е.В. Васильев, НИИЖТ); INTAB и TB–FEM (коллектив авторов под руководством Н.Н. Шапошникова, МИИТ). Программа INTAB работает только с плоскими системами.

Для работы программ необходима информация о геометрии конструкции, нагрузке, материале. Правила внесения исходных данных в программу см. [10].