











Исходные данные
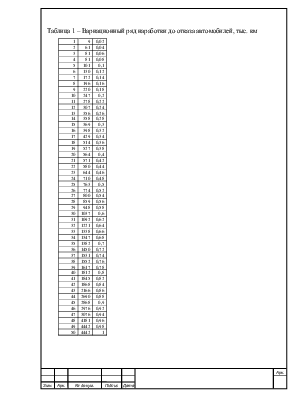
В результате наблюдений за однотипными машинами в процессе эксплуатации получается статический ряд их наработок на отказ, определяемый наработкой до отказа условных блоков.
Установить вид закона распределения
наработки на отказ и найти ![]() -процентный
ресурс машин.
-процентный
ресурс машин.
|
1347 |
527 |
710 |
564 |
220 |
1812 |
358 |
948 |
101 |
1037 |
|
3076 |
9 |
800 |
307 |
196 |
130 |
763 |
2690 |
4442 |
172 |
|
1552 |
1845 |
1868 |
514 |
859 |
1221 |
278 |
81 |
61 |
2976 |
|
774 |
81 |
1092 |
359 |
429 |
1338 |
2868 |
1450 |
1531 |
356 |
|
580 |
644 |
4442 |
398 |
571 |
247 |
1382 |
4181 |
1617 |
2166 |
Содержание
Исходные данные....................................................................................................
1. Обработка и анализ статистических данных..................................................
1.1 Статистические данные... ..............................................................................
1.2 Функция распределения...............................................................................
1.3 Поразрядная группировка полученных из опытов значений случайной величины...............................................................................................................
2. Экспоненциальное распределение............................................................
2.1 Нормальное распределение........................................................................
2.2 Логарифмически нормальное распределение..........................................
2.3 Распределение Вейбулла............................................................................
3. Закон распределения случайной величины по статистическим данным и проверка этого закона..........................................................................................
4. Показатели долговечности..............................................................................
5. Список литературы:.............................................................................................
1.Обработка и анализ статистических данных
Определение законов распределения случайных величин и нахождение параметров этих законов основываются на обработке и анализе статистических сведений об исследуемых случайных величинах.
1.1. Обработка статистических данных
Задачи математической статистики состоят в том, чтобы на основании знания некоторых свойств подмножества элементов, взятых из некоторого множества, сделать какие-то утверждения о свойствах этого множества, называемого генеральной совокупностью.
Генеральная совокупность - это совокупность объектов, содержащих все исследуемые объекты (множество).
Выборка - определённое число объектов, отобранных для получения сведений о генеральной совокупности (подмножество).
Первичные записи статистических наблюдений за случайной величиной представляют собой простой статистический ряд, в котором записываются номер опытов и значения случайной величины, наблюдавшиеся в этих опытах.
Удобным способом получить представление о распределении случайной величины Xявляется построение графика статистической функции распределени выборки (хь ..., хп)
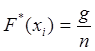 (1)
(1)
где g — число опытов, в которых случайная величина X принимала значения меньше х;
п - общее число опытов.
Статистический ряд перестраивается так, чтобы полученные значения случайной величины располагались в возрастающем порядке (вариационный ряд).
Для возрастающего ряда эмпирическая функция распределения выглядит так:
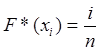 (2)
(2)
Таблица 1 – Вариационный ряд наработки до отказа автомобилей, тыс. км
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.