Закон распределения случайной величины по статистическим данным и проверка этого закона. Вариационный ряд наработки до отказа автомобилей, страница 4

                                                   S _t= 100 lg t,                                                       (12)

в которой значение t изменяются в пределах от 1 до 10. Длина шкалы при этом составляет 100 мм.

Для диапозона измерений t от 10 до 100 рассматривается величина 10t.

                                                      S_{10 t}= 100 + S_t                                                                             (13)

Для диапазона изменения t от 100 до 1000:

                                                     S _100t = 1000 + S_t                                                                        (14)

Среднее квадратичное отклонение:

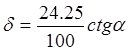                                                                                                        (15)

Числовые значения S_t берем из таблицы П.7 [1]

График функции логарифмически нормального распределения представлен на рисунке 5.

2.4 Распределение Вейбулла.

Функция распределения случайной величины:

                                                                                                       (16)

Величина S_F для вертикальной шкалы длиной 150 мм определяется после логарифмирования (16).

Логарифмируя (16) один раз, получим:

                                                     -ln[1-F(t)]=                                              (17)

Логарифмируя теперь (15) будем иметь:

                                                    -ln{-ln[1-F(t)]}=b(lnt-lna)                               (18)

Примем для F(t) крайнее значение: 0.001 и 0.999. Для этих значений размах величины -ln{-ln[1-F(t)]} составит 8,84 (от -6,91 до 1,93). Поэтому уравнение для S_F запишется в виде:

                                                 S_F=16,97ln{-ln[1-F(t)}                                        (19)

Числовое значение S_F берем из таблицы П.7 [1].

Горизонтальная шкала неравномерная и строится так же, как для логарифмически нормально распределения. Масштабный фактор K_t  находится из (10). K_t=0,034

Параметр b:

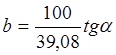                                                                                                         (20)

График функции распределения Вейбулла представлен на рисунке 6.

3. Нахождение закона распределения случайной величины по статистическим данным и проверка этого закона.

Полученная гистограмма наработок (см. рис. 2) позволят сделать предположение о том, что наработки между случайными отказами подчиняются экспоненциальному закону, плотность распределения которого по

Для нахождения свойств, определяющих надёжность машин или элементов по статистическому распределению случайной величины в выборке, должен быть найден закон распределения случайной величины, справедливый для генеральной совокупности.

Вид предполагаемого закона распределения выбирается, исходя из соображений существа случайной величины или из внешнего вида графического изображения статистического распределения.

Предположим, что наработки между случайными отказами подчиняются закон экспоненциального распределения .

По данным таблицы 2 определяется параметр потока отказов

где  m^*- оценка математического ожидания,

.

Тогда плотность распределения по

а теоретический закон распределения по (9)

Вероятность попадания случайной величины в i-й разряд по:

.

Подставляя сюда λ=0,00085 и значение α_i и β_i для каждого разряда из табл. 2, получим теоретическое значение вероятностей p_i, приведены в табл. 3.

 

Таблица 3 – Теоретическое значение вероятностей