Закон распределения случайной величины по статистическим данным и проверка этого закона. Вариационный ряд наработки до отказа автомобилей, страница 3

№	разряд		длина разряда	частота наблюдений g	частость p*	высота разряда
	α	β
1	0	350	350	12	0,24	0,69
2	350	700	350	11	0,22	0,63
3	700	1050	350	7	0,14	0,4
4	1050	1400	350	5	0,1	0,29
5	1400	2400	1000	8	0,16	0,16
6	2400	3400	1000	4	0,08	0,08
7	3400	4400	1000	3	0,06	0,06

Высота разряда гистограммы:

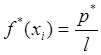                                                                                                            (3)

Общее число наблюдений:

                                                                                                         (4)

Сумма частностей:

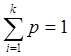                                                                                                                    (5)

Гистограмма наработки между отказами по данным статистического ряда (таблица 2) показана на рисунке 2

2 Вероятностные шкалы

     2.1 Экспоненциальное распределение.

Функция распределения случайной величины:

                                                                                                            (6)

На горизонтальной оси наносится равномерная шкала t с масштабным фактором K_t=L/∆t=150/4400=0,034

На вертикальной оси F(t) наносятся значения –ln[1-F(t)], а надписываются значения F(t) равно нулю.

Наибольшее значение F(t) удобно принимать 0.999.Тогда

  При длине вертикальной оси 150 мм:

                                                                                                 (7)

Числовое значение S_F берем из таблицы П.7 [1].

Параметр распределения:

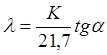                                                                                                             (8)

График функции экспоненциального распределения представлен на рисунке 3

       2.2 Нормальное распределение

При нормальном распределении

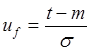                                                                                                            (9)                                  

где индекс p заменен на F,

m и - параметры распределения.

При построении шкалы Р(t) наименьшее и наибольшее значения функции распределения принимают равным 0,001 и 0,999. Тогда для u_F наименьшее значение будет -3,09 и наибольшее +3,09. Уравнение для S_F при длине шкалы 150 мм:

                                                                                                        (10)

Горизонтальная шкала равномерная K_t=0,034

Среднее квадратичное отклонение:

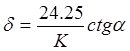                                                        ,                                               (11)

где  - угол, образованный найденной прямой осью t.

График функции нормального распределения представлен на рисунке 4

2.3 Логорифмически нормальное распределение

Для логарифмически нормального распределения величина S_F определяется по той же формуле (10) и табл. П.7, что и для нормального распределения

Горизонтальная шкала t неравномерная, логарифмическая.

Величины S_t: