Закон распределения случайной величины по статистическим данным и проверка этого закона. Вариационный ряд наработки до отказа автомобилей, страница 5

Номер разряда,i	Середина разряда, xi	Матеем. Ожидание			Теоретическая вероятность pi
1	175	42	1	0,743347073	0,256652927	0,001080525
2	525	115	0,743347073	0,552564872	0,190782201	0,00447463
3	875	122	0,552564872	0,41074748	0,141817392	0,00002329
4	1225	122	0,41074748	0,305327937	0,105419543	0,000278615
5	1900	304	0,305327937	0,130840636	0,174487301	0,001202849
6	2900	232	0,130840636	0,056068476	0,07477216	0,000365515
7	3900	234	0,056068476	0,02402674	0,032041736	0,024395199

Если значения параметров функции распределения неизвестны, то рекомендуется использовать критерий согласия Пирсона, 

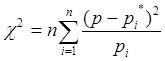                                                                                     (21)

где p_i – теоретическая вероятность попадания случайной величины наработки между отказами в каждый из n разрядов:

                                                                                                   (22)

где  - функция распределения, определяющаяся для закона экспоненциального распределения по формуле (6).

Критерий Пирсона по формуле (21):

= 50((0,001080525+0,00447463+0,00002329+0,000278615+0,01202849+0,000365515+  +0,024395199))=1,591031

Число степеней  свободы  r:

                                                   r = k-(+1)                                                         (22)

где k – число разрядов статического ряда;

 - число параметров предлагаемого распределения, для экспоненциального закона равен 1

r = 7 - (1+1 ) = 5

Теперь, используя таблицу приложения П.6[1], для =1,591031 , и r=5 получаем вероятность p=0,8491

0,8491>0,05

Следовательно, предполагаемый экспоненциальный закон не противоречит опытным данным.

       4. Показатель долговечности

Долговечность количественно оценивается с помощью двух групп показателей ресурса как показателя, связанного с наработкой объекта, и срока службы, связанного с календарной продолжительностью.

Средний ресурс (математическое ожидание ресурса) и его статистическая оценка определяются по формуле:

                                                                                                         (23)

Ресурс машины так же, как и ресурс детали, является случайной величиной, поэтому на практике ресурс определяется с заданной вероятностью у процентов, (для большинства изделий строительного и дорожного машиностроения у = 80%

Гамма-процентный ресурс в случае экспоненциального распределения находится из уравнения:

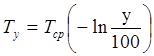                                                                                                   (24)

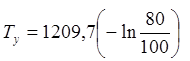=270ч.

Отсюда следует, что из выбранной партии 80% изделий проработают 270ч.

5.  Список литературы

1.  Каргин В.А. Основы теории надежности и технической диагностики:

Учеб. Пособие. – Новосибирск: Изд-во СГУПСа, 2002.- 99с.

2. СТП СГУПС 01.01.2000. Курсовой и дипломный проекты. Требования к оформлению. Новосибирск, 2000. 40с.