Расчеты на прочность в пределах упругих деформаций. Особенности расчета на прочность за пределом упругости, страница 7

.                                                (4.21)

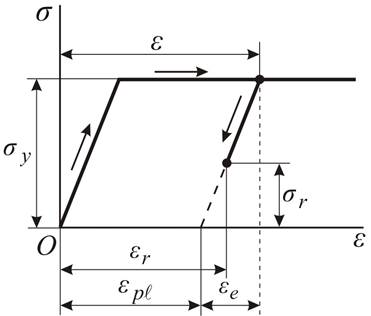
Рис. 4.13

При разгрузке происходит снижение напряжений и деформаций по линейному закону, в результате в точке остаются остаточные напряжения  и остаточные деформации , причем, . Это связано с тем, что волокна, в которых возникли пластические деформации, препятствуют упруго-напряженным волокнам восстанавливать свою первоначальную длину после разгрузки и таким путем появляются некоторые остаточные напряжения  ( - остаточный, от англ. residual).

Процесс разгрузки можно рассматривать как нагружение системы заданной нагрузкой противоположного направления.

Остаточные напряжения будут равны сумме напряжений от обоих нагружений. Они представляют собой взаимоуравновешенную систему:

.

Пример 4.5. Определить остаточные усилия и напряжения в стержнях системы (рис. 4.14 а), нагружение которой было рассмотрено в примере 4.2.

При нагружении в упругой стадии усилия в стержнях: , . При нагружении до предельного состояния соответствующая сила , а усилия в стержнях , .

Решение. Разгрузим систему, приложив к ней силу  противоположного направления (рис. 4.14 б).

Усилия разгрузки в стержнях таковы:

;   .

Остаточные усилия в стержнях равны сумме усилий при нагружении и разгрузке:

   (стержень сжат),

в

б

а

   (стержень растянут).

Рис. 4.14

Полученная система остаточных усилий (рис. 4.14 в) должна быть взаимоуравновешенной, т.е.

.

Остаточные напряжения в стержнях

.

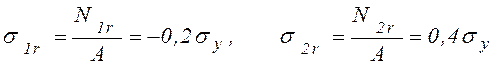Пример 4.6.Определить остаточные напряжения в балке (рис. 4.6 а), нагружение которой рассмотрено в примере 4.4. При нагружении балки до предельного состояния пластический предельный момент в опасном сечении , а напряжения во всех точках сечения равны пределу текучести , чему соответствует прямоугольная эпюра (рис. 4.6 д).

Решение. Разгрузим балку, приложив силу  противоположного направления (рис. 4.15 а).

Изгибающий момент в опасном сечении (см формулу 4.8) . Напряжения разгрузки меняются по линейному закону (рис. 4.15 в) и в крайних точках сечения с учетом формулы 4.6

б

а

г   в

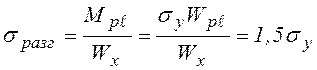
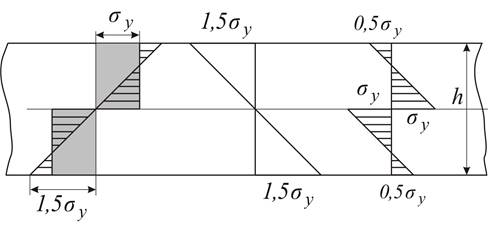
Рис. 4.15

Эпюру остаточных напряжений (рис. 4.15 г) можно получить наложением двух эпюр (рис. 4.15 б, в): прямоугольной во время нагрузки и треугольной при разгрузке. Остаточные напряжения в каждой точке сечения определяют как алгебраическую сумму напряжений в предельном состоянии  и при разгрузке:

.

Остаточные напряжения (рис. 4.15 г) в волокнах вблизи нейтрального слоя равны , а в краевых волокнах - . Распределение остаточных напряжений, представленное на рис. 4.15 г заштрихованными площадями, сводится к двум равным и противоположным парам сил величиной 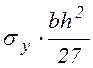, которые находятся в равновесии.

Если балка с остаточными напряжениями (рис. 4.15 г) вторично изгибается под нагрузкой той же величины и в том же направлении (рис. 4.6), то наибольшее напряжение равно , но никакой текучести не будет.

Это явление повышения несущей способности элемента путем предварительного нагружения (наклепа) и создания подходящих остаточных напряжений иногда применяется на практике.

В заключение отметим, что метод предельного равновесия применяется только в случаях действия постоянных нагрузок и не используется при временной нагрузке. Это связано с изменением свойств материала после разгрузки, что должно быть исследовано в каждом конкретном случае.