Расчеты на прочность в пределах упругих деформаций. Особенности расчета на прочность за пределом упругости, страница 4

Итак, наименьшей оказалась нагрузка, соответствующая второму варианту. Истинное значение предельной нагрузки: .

Условие прочности конструкци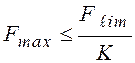и , или 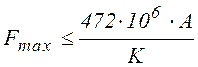. Необходимая площадь:

.

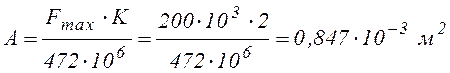Ответ: .

4.4.  Расчет статически определимой балки с учетом развития пластических деформаций

4.4.1.  Три стадии работы балки. Пластический шарнир

Рассмотрим три стадии деформирования наиболее напряженного сечения балки при возрастании нагрузки до момента исчерпания несущей способности.

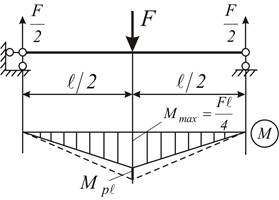
Пример 4.4. Балка прямоугольного сечения из упругопластического материала нагружена силой F (рис. 4.6 а). Изгибающий момент имеет наибольшее значение в среднем сечении балки: .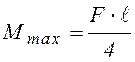

В упругом состоянии материала нормальные напряжения в поперечном сечении линейно изменяются по высоте балки. При увеличении нагрузки крайние волокна первыми достигнут предела текучести , что считается опасным с позиции упругого расчета (рис. 4.6 в). Соответствующую нагрузку  и изгибающий момент  опасный с позиции упругого расчета, находят исходя из условия 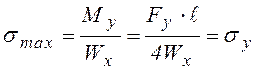. Откуда:

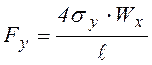;     .                                (4.6)

г

в

б

а

д

При дальнейшем увеличении нагрузки наступает упругопластическая стадия деформирования балки. Зона текучести будет распространяться глубже по сечению, захватывая новые волокна, но в средней части сечения еще сохранится упругое ядро высотой h (рис. 4.6 г).

е

Рис. 4.6

Предельное состояние наступает тогда, когда пластические деформации распространятся по всему сечению, что отражает соответствующая прямоугольная эпюра напряжений (рис. 4.6 д). Процесс деформирования материала по всему сечению полностью переходит в пластическую стадию.

Состояние поперечного сечения, при котором во всех его точках развиваются пластические деформации, называют пластическим шарниром (рис. 4.6 е).

При этом несущая способность балки считается исчерпанной, т.к. прогиб балки увеличивается постоянной нагрузке , т.е. балка превращается в механизм. В поперечном сечении, где образовался пластический шарнир, внутренний момент обозначим  и назовем пластическим предельным моментом. Для данной балки в соответствии с эпюрой моментов (рис. 4.6 а) 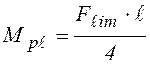, откуда предельная нагрузка .

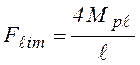Итак, предельное состояние статически определимой балки характеризуется возникновением одного пластического шарнира.

4.4.2.  Расчёт пластического предельного момента

Оценим несущую способность балки симметричного сечения в предельном состоянии.

Внутренний момент  определяется как момент элементарных сил  относительно оси х (рис. 4.7).

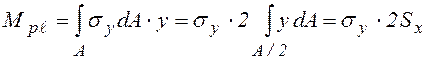, где  - статический момент площади полусечения относительно нейтральной линии.

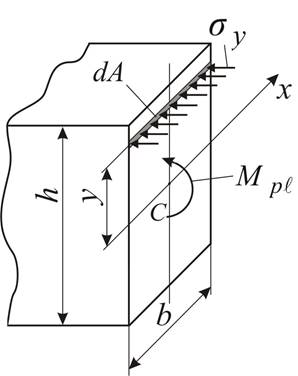
Рис. 4.7

Величина

                                                   (4.7)

называется пластическим моментом сопротивления (по аналогии с осевым ). Тогда предельный момент равен:

,                                         (4.8)

а предельная нагрузка такова:

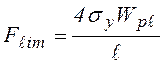 .                                       (4.9)

Для прямоугольного сечения пластический момент сопротивления

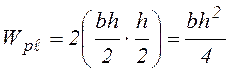,                              (4.10)

в то время как осевой

.

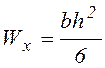Отношение предельного момента  к моменту , который считается опасным с позиции упругого расчета, называется коэффициентом формы сечения.

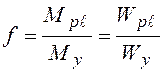.                                        (4.11)

Для прямоугольного сечения:

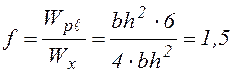.                             (4.12)