Расчеты на прочность в пределах упругих деформаций. Особенности расчета на прочность за пределом упругости, страница 2

Отсюда название расчета, принятое в строительной практике: метод предельного равновесия.

В качестве условия прочности выдвигается требование того, чтобы наибольшая рабочая (допускаемая) нагрузка составляла некоторую часть от предельной

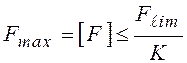 ,                                              (4.2)

где К - коэффициент запаса прочности.

С пластическими деформациями связан расчет деталей, «работающих» длительное время в условиях высоких температур: диски и лопатки паровых и газовых турбин, трубы паровых котлов, элементы реактивных двигателей и др. С учетом пластических деформаций рассчитываются сильно напряженные элементы конструкций, например оболочки ракетных двигателей.

Строительные нормы и правила регламентируют учет пластических деформаций при расчете строительных конструкций. Расчеты на прочность по методу предельного равновесия позволяют использовать дополнительные прочностные ресурсы, которые не берутся во внимание при расчетах в упругой стадии. Это дает возможность создавать более экономичные конструкции за счет снижения их материалоемкости. Учет развития пластических деформаций позволяет повысить несущую способность элементов конструкций и добиться равнопрочности отдельных частей и элементов конструкции.

4.3.  Расчет предельной нагрузки в стержневых системах,

«работающих» на осевую нагрузку

4.3.1.  Статически определимые системы

Пример 4.1.Абсолютно жесткий брус ОВ закреплен в шарнире О и подвешен на стержне СВ из упругопластического материала (рис.4.3). Определить предельную нагрузку .

б

а

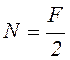Решение. При  стержень СВ работает на растяжение в упругой стадии. Усилие в стержне , а напряжение 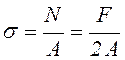. Опасное состояние наступит, когда напряжения достигнут предела текучести 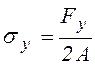, при этом соответствующая сила .

Рис. 4.3

Так как при растяжении (сжатии) напряженное состояние является однородным, то напряжения во всех точках сечения одновременнодостигнут предела текучести . Это вызовет неограниченную пластическую деформацию стержня – и брус ОВ свободно повернется вокруг шарнира О, т.е. система превратится в механизм. Такое состояние будет предельным, а предельная нагрузка равна

.

Таким образом, в статически определимых системах результат расчета по предельной нагрузке совпадает с результатом расчета по напряжениям в опасной точке.

4.3.2. Статически неопределимые системы

В статически неопределимых системах при растяжении, сжатии переход к методу предельного равновесия дает существенный эффект в плане увеличения несущей способности конструкции по сравнению с упругим расчетом.

в

б

а

Пример 4.2. Жесткий брус ОВ (рис. 4.4 а) закреплен в шарнире О и подвешен на двух одинаковых стержнях (тягах) с площадью сечения А. Определить предельную нагрузку .

Схема предельного равновесия

            

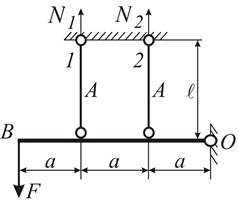
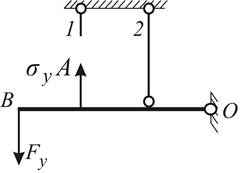
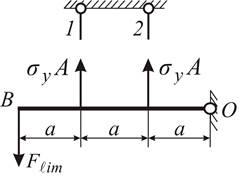
Рис. 4.4

Решение. Проанализируем работу этой системы при нагружении ее плавно возрастающей нагрузкой F.

Система (рис. 4.4 а) один раз статически неопределима. В упругой стадии работы напряжения в обоих стержнях меньше предела текучести . Для определения этих напряжений нужно раскрыть статическую неопределимость (см. пример 3.4). Усилия в стержнях получаются равными 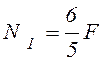, 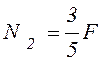. Напряжение в первом стержне оказывается большим, чем во втором .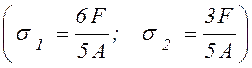

Увеличение нагрузки приводит к пропорциональному росту напряжений в стержнях. С позиции упругого расчета опасное состояние системы наступит, когда в более напряженном первом стержне напряжение достигнет предела текучести, т.е. 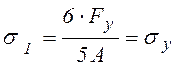. Откуда находим соответствующую нагрузку: