Расчеты на прочность в пределах упругих деформаций. Особенности расчета на прочность за пределом упругости, страница 6

Этот критерий позволяет рассчитывать стальные балки не только из условия появления пластических деформаций или условия образования пластического шарнира, но и в упруго – пластической стадии (рис. 4.6 г) работы материала (). Внутренний момент в сечении , который допускается по развитию пластических деформаций, полагают равным , где  для прямоугольного сечения. При этом отпадает необходимость вычисления , т.к. СНиП содержит таблицу значений коэффициента С, которые используются в качестве множителя к упругому моменту сопротивления .

Условие прочности при расчете по ограниченной пластической деформации записывается в виде

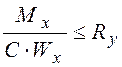.                                                (4.16)

4.5. Расчет статически неопределимой балки с учетом развития

пластических деформаций

В статически неопределимых балках возникновение пластического шарнира, как правило, не приводит к исчерпанию их несущей способности.

Рассмотрим один раз статически неопределимую балку (рис. 4.10 а) прямоугольного сечения.

а

На упругой стадии деформирования балки эпюра изгибающих моментов имеет вид, показанный на рис. 4.10 б (см. пример 3.3). Опасным является сечение D под сосредоточенной силой, где .

б

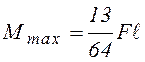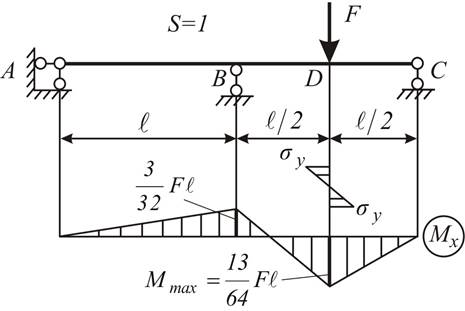
Рис. 4.10

При возрастании нагрузки напряжения равные пределу текучести  появятся в первую очередь в крайних точках сечения D. При этом соответствующий изгибающий момент в точке D и значение нагрузки находятся так:

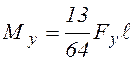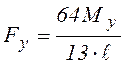,      .                            (4.17)

Дальнейший рост нагрузки приведет к образованию пластического шарнирав сечении D (рис. 4.11 а), где соответствующий изгибающий момент будет равен

.                                    (4.18)

Эпюра изгибающих моментов показана на рис. 4.11б.

При дальнейшем возрастании нагрузки балка работает как статически определимая, нагруженная в промежуточном шарнире Dувеличивающейся сосредоточенной силой и постоянным моментом .

б

а

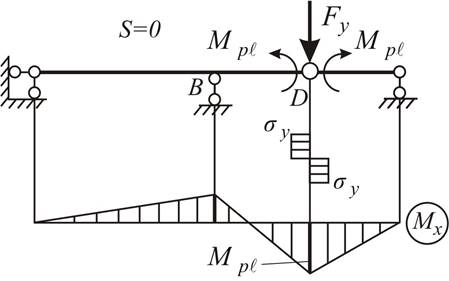
Рис. 4.11

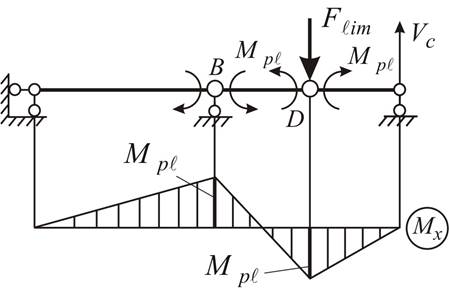
Предельное состояние наступит при возникновении второго пластического шарнира в сечении В. Балка обратится в механизм (рис. 4.12 а). Соответствующая эпюра изгибающих моментов (рис. 4.12 б) показывает, что произошло перераспределение, или, как говорят, уравнивание моментов в наиболее напряженных сечениях D и В.

Для расчёта предельной силы F рассмотрим схему предельного равновесия балки (рис. 4.12 а) и составим уравнения равновесия:

.

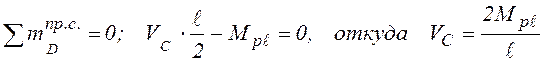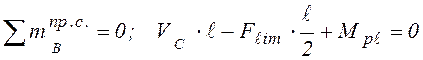, откуда

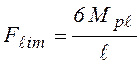.                                             (4.19)

Отношение предельной силы F к силе

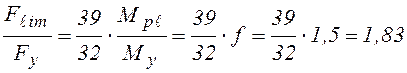,                    (4.20)

где  для прямоугольного сечения.

Как видно (формула 4.20), несущая способность балки по сравнению с данными обычного упругого расчета возросла на 83%.

Рис. 4.12

Обратим внимание на то, что для статически определимой балки того же сечения аналогичное соотношение равно (см. формулу 4.12)

.

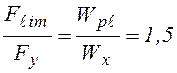Таким образом, один раз статически неопределимая балка превратилась в кинематически изменяемую при образовании двух пластических шарниров. Несущая способность дважды статически неопределимой балки обычно оказывается исчерпанной при образовании трех пластических шарниров.

Следует отметить, что количество пластических шарниров, которые необходимы для перехода балки в предельное состояние, далеко не всегда должно быть на единицу выше степени статической неопределимости. Многопролетная балка теряет несущую способность, если хотя бы один из ее пролетов обращается в кинематически изменяемую систему.

4.6. Остаточные напряжения

Рассмотрим вопрос о напряжениях, которые остаются в системе после снятия нагрузки.

При нагружении вслед за упругими деформациями  развиваются пластические . Так что в некоторой точке суммарная деформация будет, (см. рис. 4.13), такова: