Расчеты на прочность в пределах упругих деформаций. Особенности расчета на прочность за пределом упругости, страница 5

Т.е. учет образования пластического шарнира позволяет повысить несущую способность балок прямоугольного сечения в 1,5 раза по сравнению с обычным расчетом в упругой области.

Для прокатных двутавровых балок пластический момент сопротивления определяется из таблиц сортамента через статический момент как , при этом . Очевидно, коэффициент f тем меньше, чем рациональнее распределен материал по высоте сечения с точки зрения упругого расчета.

4.4.3.  Положение нейтральной линии при образовании

пластического шарнира

Рассмотрим сечение балки с одной осью симметрии (рис. 4.8 а).

в

б

а

В упругой стадии эпюра  линейна и нейтральная линия совпадает с осью х (рис. 4.8 б). При образовании пластического шарнира нейтральная линия n-n смещается от центра тяжести С в сторону более массивной части (рис. 4.8 а, в).

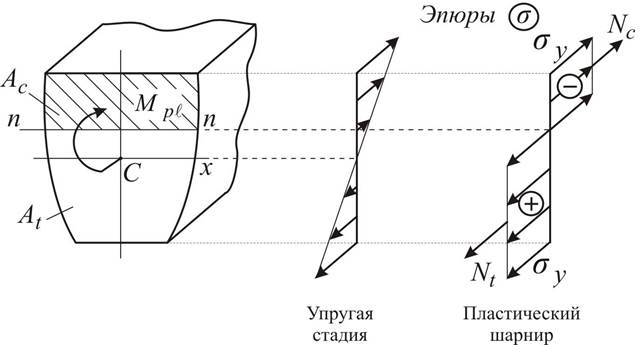
Рис. 4.8

Действительно, все сечение делится на растянутую часть  силой  и сжатую  силой . Так как суммарная продольная сила при изгибе равна нулю, то из условия  следует, что

.

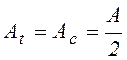При образовании пластического шарнира нейтральная линия делит площадь сечения на две равновеликие части(рис. 4.8 а).

В этом случае пластический момент сопротивления –

 ,                                           (4.13)

где  - статический момент растянутой части сечения относительно нейтральной линии n-n;  - абсолютная величина статического момента сжатой части сечения относительно нейтральной линии n-n.

4.4.4.  Определение длины пластической зоны, примыкающей

к пластическому шарниру

В состоянии пластического шарнира (рис. 4.9 а) деформация в крайних волокнах в  раз превышает упругую деформацию. При этом упругое ядро практически исчезает. Области пластического течения волокон заштрихованы на балке.

а

Обозначим длину пластической зоны  (рис. 4.9 а).

б

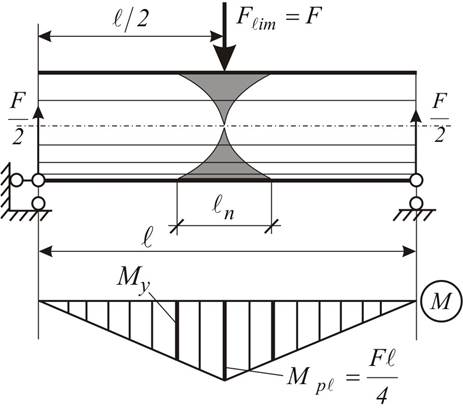
Рис. 4.9

Изгибающий момент в начале пластической зоны  (рис. 4.9 б):

.

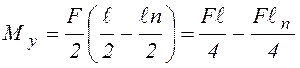Предельный момент в балке 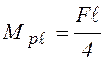, тогда:

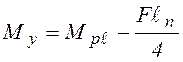 или 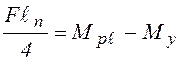, откуда:

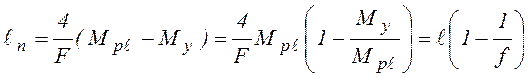.                   (4.14)

Для балки прямоугольного сечения с коэффициентом формы сечения  длина пластической зоны равна

.

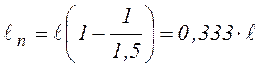Для двутавровой балки 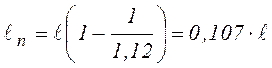, т.е. значительно меньше, чем для прямоугольной.

Наличие пластической зоны по длине может привести к потере устойчивости стенки и листов сжатого пояса сечения двутавровой балки еще до того, как возникнет пластический шарнир.

Примечание. Выражение (4.14) для расчёта  применимо только для данной шарнирно опертой балки с силой, приложенной посредине.

4.4.5.  Расчет по ограниченной пластической деформации

Метод предельного равновесия имеет существенный недостаток: он позволяет судить только о напряженном состоянии за пределом текучести, в то время как уровень деформации остается неизвестным. Между тем изменение геометрической формы конструкции допустимо лишь до некоторого предела, зависящего от назначения конструкции, степени ее ответственности и условий эксплуатации.

Поэтому глава СНиПа 2.02.01-83 вводит критерий ограничения пластической деформации стальных балок

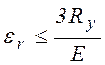,                                                  (4.15)

где  - относительное остаточное удлинение в долях единицы;  - расчетное сопротивление стали растяжению и сжатию, установленное по пределу текучести  ( -нормативное сопротивление); Е - модуль упругости прокатной стали, равный 206 ГПа.