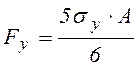Расчеты на прочность в пределах упругих деформаций. Особенности расчета на прочность за пределом упругости, страница 3

.                                             (4.3)

С этого момента начинается вторая стадия «работы» - упругопластическая, при которой дальнейшее увеличение нагрузки сопровождается ростом усилия  во втором стержне при постоянном значении () в первом. При этом данная система становится статически определимой, т.к. усилие в пластически деформируемом первом стержне известно (рис. 4.4 б). Усилие в упругом стержне «2» можно определить из уравнения равновесия (сумма моментов всех сил, действующих на брус ОВ относительно точки О, равна нулю). Второй стержень, находясь в упругом состоянии, будет ограничивать рост пластических деформаций в первом стержне.

Третья стадия работы - предельное состояние наступит в то время, когда при увеличении нагрузки напряжение во втором стержне достигнет предела текучести. В этом состоянии деформации стержней будут неограниченно возрастать при постоянной нагрузке , а усилия в стержнях равны:

.                                    (4.4)

Предельное состояние системы характеризуется ее превращением в механизм (потерей кинематической неизменяемости), т.к. возможен свободный поворот бруса ОВ вокруг опорного шарнира О.

Значение предельной нагрузки можно определить из уравнения предельного равновесия системы(рис. 4.4 в).

, откуда

.                                             (4.5)

Найдем отношение предельной силы  к нагрузке , опасной с позиции упругого расчета:

.

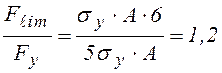Т.е. дополнительный резерв несущей способности конструкции за счет перехода к расчету с учетом пластических деформаций материала будет равен 20%.

Вывод:Предельное состояние стержневой системы, 1 раз статически неопределимой, наступило при возникновении текучести в двух стержнях. Последовательное исчерпание несущей способности отдельных стержней приводит к предельному случаю полного исчерпания несущей способности системы в целом.

Пример 4.3. Для конструкции (рис. 4.5 а) по методу предельного равновесия определить требуемое значение площади А. Пределы текучести для материалов стержней: 1) алюминий – 200 МПа; 2) медь – 160 МПа; 3) сталь – 280 МПа. Нагрузка 200 кH, требуемый коэффициент запаса .

Решение. Система 1 раз статически неопределима, поэтому ее несущая способность исчерпается при возникновении пластических деформаций в двух стержнях. Чтобы установить, в какой последовательности стержни будут переходить в состояние текучести, необходимо раскрыть статическую неопределимость системы в упругой стадии работы или применить кинематический метод. Сущность его заключается в последовательном рассмотрении всевозможных  вариантов исчерпания несущей способности системы. Для каждого из них составляются уравнения предельного равновесия и определяются соответствующие значения предельной нагрузки. Очевидно, что меньшая из них будет истинной предельной нагрузкой.

а

г

в

б

Применим этот метод к заданной системе.

               

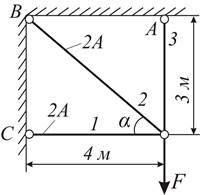
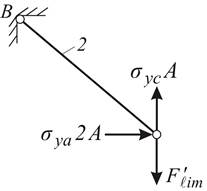
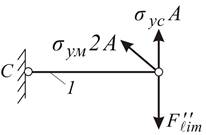
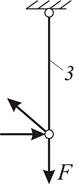
Рис. 4.5

Вариант 1 (рис. 4.5 б): предположим, что текучесть возникла в 1-ом и 3-ем стержнях. Тогда уравнение предельного равновесия запишется так:

;

, откуда

.

Вариант 2 (рис. 4.5 в): предположим, что текучесть возникла во 2-ом и 3-ем стержнях. Уравнение предельного равновесия:

;

, откуда

.

Вариант 3 (рис. 4.5 г) - предполагаем, что текучесть возникла в 1-ом и 2-ом стержнях. Это состояние не является предельным, т.к. сила Fсовпадает с осью стержня 3, а если он находится в упругой стадии, то при росте нагрузки усилие в нем будет возрастать, а  несущая способность системы окажется исчерпанной лишь тогда, когда текучесть возникнет и в этом стержне.