Уравнение равновесия поршня гидроцилиндра. Расчет основных размеров гидроцилиндра и подачи насоса. Определение расходов рабочей жидкости в гидравлических линиях системы гидропривода, страница 7

Вычисленное давление на выходе из насоса несколько меньше его задан­ного номинального значения и равного ему (2,5 МПа) давления нагнетания (на выходе) выбранного трехвинтового насоса МВН-6 (см. п. 2.6). Следователь­но, зтот насос выбран правильно, т.к. он обеспечивает давление, необходимое для работы заданной системы объемного гидропривода.

4.7 Как уже упоминалось в п. 4.2, определение потерь давления в напорной 2 и сливной 3 гидролиниях выполняется по упрощенному уравнению Бернулли (4.6), давления в котором целесообразно рассматривать избыточные. Рассмот­рим напорную гидролинию. Первое живое сечение следует брать перед штуце­ром присоединения гидролинии 2 к нагнетательной линии насоса (р₁ = р_вых), а второе - внутри гидроцилиндра возле поверхности S_p его поршня (р₂ = р_р).

Таким образом, упрощенное уравнение Бернулли (4.6) для напорной гид­ролинии имеет вид

                                                                                   (4.14)

где  - суммарные потери давления на трение в напорной гидро­линии, Па;

 - суммарные потери давления в местных сопротивлениях напор­ной гидролинии, Па.

Согласно схеме объемного гидропривода (рисунок 1), потери давления на трение и в местных сопротивлениях напорной гидролинии между выбранными живыми сечениями будут следующие:

- на трение по длине гидролинии ( ∆р_{тр н} );

- в четырех штуцерных соединениях (4 • ∆р_{тр н} );

- в стандартном тройнике при прямом проходе жидкости и разделении по­токов (∆р_{трк н});

- в канале (линии) распределителя со стороны нагнетания (∆р_р.н);

- при внезапном расширении потока на выходе из гидролинии в рабочую полость гидроцилиндра (∆р_вых.н).

Таким образом, из уравнения (4.14) следует

.

Отметим, что выражение в скобках – это суммарные потери давления в напорной гидролинии.

Окончательный вид это уравнение приобретает после использования формул (4.7) и (4.8)

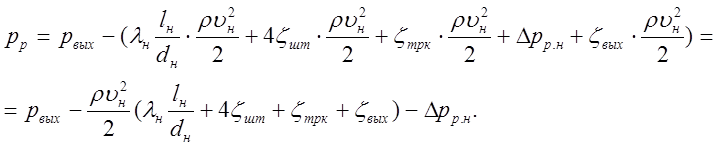(4.15)

Полученное уравнение дает возможность определить давление в рабочей полости гидроцилиндра р_р после вычисления входящих в него потерь давления.

4.8 Для сливной гидролинии первое живое сечение следует брать внутри гидроцилиндра возле поверхности S_сл его поршня (р₁ = р_сл), а второе - на сво­бодной поверхности жидкости в гидробаке (р₂ = 0, т.к. оно избыточное, а бак открыт в атмосферу).

Упрощенное уравнение Бернулли (4.6) при этом примет вид

                                                  ,                                                         (4.16)

где       - суммарные  потери  давления  на трение   в  сливной   гидро­линии, Па;

           - суммарные потери давления в местных сопротивлениях сливной гидролинии, Па.

Исходя из заданной схемы объемного гидропривода, потери давления на трение и в местных сопротивлениях сливной гидролинии между выбранными живыми сечениями - такие:

- при внезапном сужении потока на входе в гидролинию из сливной по­лости гидроцилиндра ();

- на трение по длине гидролинии ();

- в семи штуцерных соединениях ( 7 •);

- в четырех плавных поворотах (4 •);

- в канапе (линии) распределителя со стороны слива ();

-в дросселе ();

-в фильтре ();

- при внезапном расширении потока на выходе из гидролинии в бак ()

С учетом изложенного выше уравнение (4.16) становится следующим

.

Правая часть записанного уравнения — это суммарные потери давления в сливной гидролинии.

Использовав формулы (4.7) и (4.8), придадим эюму уравнению оконча­тельный вид

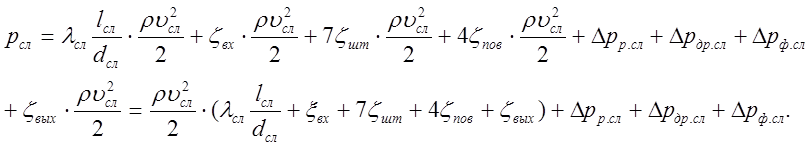  (4.17)

Уравнение (4.17) позволяет после определения значений входящих в него потерь давления вычислить давление в сливной полости гидроцилиндра р_сл.

В зависимостях (4.15) и (4.17) неизвестными являются: коэффициенты по­терь на трение по длине обеих гидролиний λ_н и λ_сл, коэффициенты сопротивле­ния поворотов ζ_пов и тройника ζ_трк, а также потери давления в дросселе  ∆р_др.сл, фильтре  ∆р_ф.сл и каждом из каналов распределителя ∆р_р.н и∆р_р.сл.

4.9 Как и при расчете всасывающей гидролинии, для определения коэф­фициентов потерь на трение в первую очередь необходимо знать числа Рейнольдса потока в соответствующих гидролиниях, окончательные значения кото­рых приведены в п. 3.6, - Re_н = 8268, Re_сл = 7813.

В напорной и сливной гидролиниях течение турбулентное. По­этому необходимо знать также и величину относительной гладкости внутренней поверхности гидролинии

,

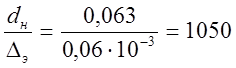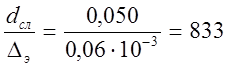
Для получения численного значения коэффициента λ_н, соответствующего Re_н = 8268 и d_H/∆_э=1050, а также , соответствующего Re_сл =7813 и d_сл/∆_э=833 воспользуемся представленными в [18] на с. 90 гра­ф иками ВТИ. По ним

λ_н =0,0341,

                                                                   =0,0347.

По графикам видно также, что течение происходит в переходной области определения коэффициента λ.

4.10 На с. 7 для коэффициента сопротивления поворотов гидролиний дан интервал значений (ζ_пов =0,14...0,98 в зависимости от геометрических характе­ристик поворотов). Примем

ζ_пов  =0,21.

Коэффициент сопротивления стандартного тройника, расположенного в самом начале гидролинии 2, при прямом проходе жидкости и разделении пото­ков возьмем из приведенной в [21] на с. 47 таблицы 4.19, определив сначала со­отношение расходов потоков в боковом ответвлении Q_дp и до разделения Q_нac

.

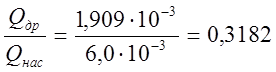При таком соотношении

ζ_трк =0,9.

4.11 Как следует из [8] — с. 311 - гидравлические распределители предна­значены для изменения направления потока рабочей жидкости в двух или более гидролиниях в результате внешнего управляющего воздействия. Они подразде­ляются по числу подводимых внешних гидролиний и числу фиксированных по­зиций запорно-регулирующего органа. В машиностроении в основном приме­няются гидрораспределители кранового или золотникового типа.

По гидравлической схеме задания система объемного гидропривода долж­на иметь четырехлинейный двухпозиционный (4/2) распределитель (согласно [13] это могут быть распределители типа Г71-2 и БМГ).