Коэффициент кинематической вязкости v берется из представленной в [7] на с. 10 таблицы 2 или из таблицы 1.1, имеющейся в [20] на с. 12, где они приведены для обычной для гидроприводов температуры рабочей жидкости, равной 50 ºС. Для заданной рабочей жидкости (масло АМГ-10) v = 10·10-6 м2/с = 10-3 м2/с.
Согласно формуле (3.3)
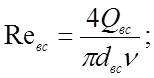
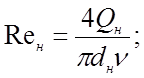
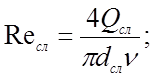
Определим с помощью этих формул режимы течения жидкости в рассматриваемых гидролиниях
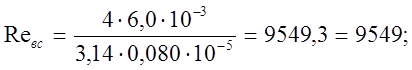
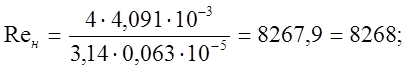
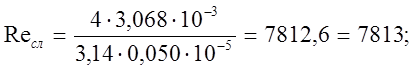
Как видим, Reсл < Reвс < Reн > 4000, т.е. во всасывающей, сливной и напорной гидролиниях обеспечивается турбулентный режим течения.
3.6 В результате расчетов, выполненных в п. 3.5, окончательно принимаем следующие значения внутренних диаметров гидролиний и чисел Рейнольдса:
dвс=80 мм = 0,080 м, Reвс=9549;
dн = 63 мм = 0,063 м, Reн = 8268;
dсл = 50 мм = 0,050 м, Reсл = 7813.
3.7 Определим, воспользовавшись формулой (3.2), средние скорости течения рабочей жидкости во всасывающей, напорной и сливной гидролиниях при значениях их внутренних диаметров, принятых в п. 3.6,
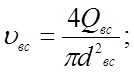
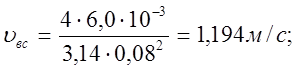
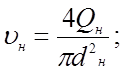
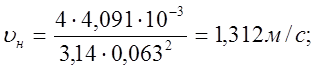
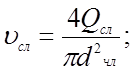
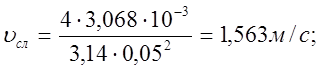
4 ОСОБЕННОСТИ ПРИМЕНЕНИЯ УРАВНЕНИЯ БЕРНУЛЛИ
СИСТЕМЫ ОБЪЕМНОГО ГИДРОПРИВОДА,
ОПРЕДЕЛЕНИЕ ПОТЕРЬ ДАВЛЕНИЯ В ГИДРОСИСТЕМЕ,
ВЫБОР ГИДРАВЛИЧЕСКОЙ АППАРАТУРЫ И ФИЛЬТРА
4. 1 Определение потерь напора (давления) в трубопроводах (гидравлических потерь) - это задача их гидравлического расчета, основанного на использовании уравнения Бсрнулли для потока реальной жидкости (двух его живых сечений 1-1 и 2-2) -см. уравнение (1.55) на с. 47 в [18]:
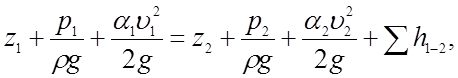 (4.1)
(4.1)
где z - расстояние от центра тяжести живого сечения до выбранной горизонтальной плоскости сравнения, м;
р - давление в центре тяжести живого сечения, Н/м2;
ρ- плотность рабочей жидкости, кг/м3 ;
g - ускорение силы тяжести, м/с2;
α- коэффициент Кориолиса;
υ - средняя скорость в живом сечении, м/с.
Геометрический смысл слагаемых уравнения Бернулли для потока вязкой жидкости заключается в следующем:
z - геометрический напор (м) в центре тяжести живого сечения, определяемый по отношению к выбранной горизонтальной плоскости сравнения;
![]() - пьезометрический напор
(м) потока жидкости в центре тяжести живого сечения;
- пьезометрический напор
(м) потока жидкости в центре тяжести живого сечения;
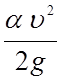 -
скоростной (динамический) напор (м) потока жидкости в живом сечении;
-
скоростной (динамический) напор (м) потока жидкости в живом сечении;
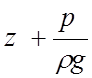 -
статистический напор (м) потока жидкости в живом сечении;
-
статистический напор (м) потока жидкости в живом сечении;
H =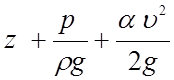 - полный напор (м) потока жидкости в живом сечении;
- полный напор (м) потока жидкости в живом сечении;
![]() - суммарные
потери полного напора (м) в потоке жидкости на участке между живыми сечениями
1-1 и 2-2 (гидравлические потери).
- суммарные
потери полного напора (м) в потоке жидкости на участке между живыми сечениями
1-1 и 2-2 (гидравлические потери).
Известен также более компактный вид уравнения Бернулли
H1 = H2 + ![]() .
.
Гидравлические потери в общем случае — это суммарные потери напора на трение по длине трубопровода Σhmp и в местных сопротивлениях Σhм
![]() (4.2)
(4.2)
Энергетический смысл слагаемых уравнения Бсрнулли для поюка вязкой жидкости:
z - удельная потенциальная энергия положения (м) потока жидкости в живом сечении, определяемая по вертикальной координате его центра тяжести;
![]() - удельная
потенциальная энергия давления (м) потока жидкости в живом сечении,
определяемая в его центре тяжести;
- удельная
потенциальная энергия давления (м) потока жидкости в живом сечении,
определяемая в его центре тяжести;
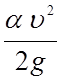 - удельная
кинетическая энергия (м) потока жидкости в живом сечении;
- удельная
кинетическая энергия (м) потока жидкости в живом сечении;
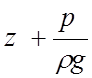 - удельная
потенциальная энергия (м) потока жидкости в живом сечении;
- удельная
потенциальная энергия (м) потока жидкости в живом сечении;
H =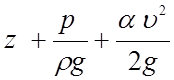 - полная удельная энергия (м) потока жидкости в живом
сечении;
- полная удельная энергия (м) потока жидкости в живом
сечении;
![]() - суммарные потери полной удельной энергии (м) в потоке
жидкости на участке между живыми сечениями 1-1 и 2-2.
- суммарные потери полной удельной энергии (м) в потоке
жидкости на участке между живыми сечениями 1-1 и 2-2.
В уравнении Бернулли (4.1) полная удельная энергия жидкости — это ее полная энергия, отнесенная к весу жидкости ρgV , т.е. приходящаяся на единицу веса протекающей жидкости.
4.2. Системы объемного гидропривода обычно работают при значительных избыточных давлениях, создаваемых объемными насосами (до 250 МПа согласно ряду номинальных давлений, установленному ГОСТ 12445-80, - см. с. 8 в [20]; от 1,6 до 10 МПа - в заданиях настоящей курсовой работы).
Полное приращение энергии жидкости в объемном насосе обычно относят к объему жидкости V - [18] на с. 274. При этом полная удельная энергия жидкости и ее слагаемые выражаются в единицах давления и являются приходящимися на единицу объема жидкости. Следовательно, уравнение Бернулли (4.1), а также зависимость (4.2) будут иметь вид:
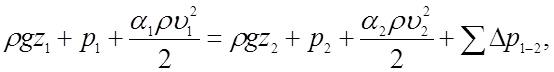 (4.3)
(4.3)
![]() (4.4)
(4.4)
Слагаемые уравнения Бернулли (4.3) и уравнения (4.4) - это давления и потери давления. Они имеют следующий энергетический смысл:
ρgz — удельная потенциальная энергия положения (Па) потока жидкости в живом сечении, определяемая по вертикальной координате его центра тяжести; р — удельная потенциальная энергия давления (Па) потока жидкости в живом сечении, определяемая в его центре тяжести;
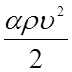 - удельная
кинетическая энергия (Па) потока жидкости в живом сечении;
- удельная
кинетическая энергия (Па) потока жидкости в живом сечении;
![]() - суммарные потери
полной удельной энергии (Па) в потоке жидкости на участке между живыми
сечениями 1-1 и 2-2;
- суммарные потери
полной удельной энергии (Па) в потоке жидкости на участке между живыми
сечениями 1-1 и 2-2;
![]() - суммарные потери
полной удельной энергии (Па) на трение по
- суммарные потери
полной удельной энергии (Па) на трение по
длине гидролинии в потоке жидкости на участке между живыми сечениями 1-1 и 2-2;
![]() - суммарные потери
полной удельной энергии (Па) в местных сопротивлениях в потоке жидкости на
участке между живыми сечениями 1-1 и 2-2. Объемные насосы предназначены в
основном для создания значительных приращений давления, поэтому приращением
кинетической энергии в них обычно пренебрегают (как и приращением удельной
потенциальной энергии положения) - см. [18] на с. 274. Следовательно, давление
насоса представляет собой разность между избыточным давлением на выходе из
насоса (в начале гидролинии 2) рвых и давлением на входе в
него (в конце гидролинии 1) рвх или pвак.вх
- суммарные потери
полной удельной энергии (Па) в местных сопротивлениях в потоке жидкости на
участке между живыми сечениями 1-1 и 2-2. Объемные насосы предназначены в
основном для создания значительных приращений давления, поэтому приращением
кинетической энергии в них обычно пренебрегают (как и приращением удельной
потенциальной энергии положения) - см. [18] на с. 274. Следовательно, давление
насоса представляет собой разность между избыточным давлением на выходе из
насоса (в начале гидролинии 2) рвых и давлением на входе в
него (в конце гидролинии 1) рвх или pвак.вх
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.