Уравнение равновесия поршня гидроцилиндра. Расчет основных размеров гидроцилиндра и подачи насоса. Определение расходов рабочей жидкости в гидравлических линиях системы гидропривода, страница 6

                                                            р_нас = р_вых - р_вх ;

                                                            р_нас = р_вых + р_вак.вх ,                                                    (4.5)

где     р_вх - избыточное давление на входе в насос, Па;

          р_вак.вх - вакуум (отрицательное избыточное давление) на входе в насос, Па.

По тем же соображениям пренебрегают вышеупомянутыми удельными энергиями и при расчете гидравлических линий.

Согласно [20] - с. 7 - уравнение Бернулли в полном виде (4.3) использует­ся только для расчета всасывающих гидролиний насосов, а в остальных случаях расчет ведут по упрощенному уравнению Бернулли, полученному из уравнения (4.3), пренебрегая слагаемыми ρgz и αρυ²/2,

                                            .                                                                 (4.6)

Таким образом, определение потерь давления в рассматриваемой гидросистсме сводится к их вычислению с помощью полного уравнения Бернулли (4.3) во всасывающей гидролинии 1, а с помощью упрощенного уравнения Бер­нулли (4.6) - в напорной 2 и сливной 3 гидролиниях.

4.3. Дая определения потерь давления на трение по длине гидролиний ис­пользуется формула Дарси-Вейсбаха — см. формулу (1.60) в [ 18] или в [7] фор­мулу 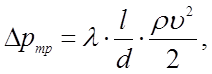(4.7)

                                                                                                             (4.7)

где     λ-коэффициент потерь на трение по длине гидролинии;

l- длина гидролинии, м;

d- внутренний диаметр гидролинии, м.

Коэффициент λ, в общем случае зависящий от числа Рейнольдса и относи­тельной эквивалентной шероховатости внутренней поверхности гидролинии Δ_э/d,- см. с. 85 в [18] - может зависеть и только от одного из этих параметров.

Определяется коэффициент λ по формулам или по графикам ВТИ (при турбу­лентном режиме течения).

4.4. Потери давления в местных сопротивлениях определяются с помощью формулы Вейсбаха - см. с. 49 в [ 18] или в [7] формулу (4.11)

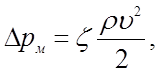                                                                                                                     (4.8)

где ζ - коэффициент сопротивления рассматриваемого местного сопротивления.

4.5. Выполним расчет потерь давления во всасывающем трубопроводе 1 , определив при этом избыточное давление на входе в насос, необходимое в будущем для выбора типа насоса. Воспользуемся уравнением Бернулли (4.3), взяв за первое живое сечение свободную поверхность рабочей жидкости в от­крытом гидробаке Б, находящемся под атмосферным давлением р_ат, а второе - в конце гидролинии 1 непосредственно после штуцерного соединения на входе в насос. Предположив расположение обоих живых сечений в одной горизонталь­ной плоскости (действительное расположение в задании не оговорено), можно записать

z₁ = z₂.

Очевидно, что скорость рабочей жидкости на ее свободной поверхности в гидробаке

υ₁≈0 .

        Абсолютное давление на находящейся под атмосферным давлением (р_ат) свободной поверхности жидкости

р₁ =р_ат .

Во втором живом сечении:

- абсолютное давление р₂ - это давление р_{абс вх} на входе в насос;

- скорость υ₂ - это скорость υ_вс;

- коэффициент Кориолиса α₂ следует обозначить как α_вс;

- потери следует обозначить как .

Таким образом, с учетом результатов выполненного анализа уравнения (4.3), оно принимаем вид

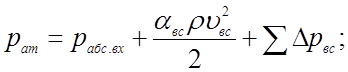
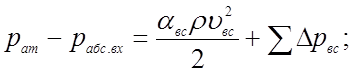
Известно, что р_ат - р_абс = р_вак , поэтому левая часть последнего уравне­ния - это р_вак.вх , а само уравнение с учетом этого будет таким

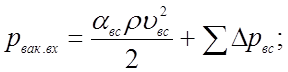                                                                                                (4.9)

Следовательно, на входе в насос будет вакуум, т.е. отрицательное избы­точное давление.

Согласно схеме и исходным данным потери давления во всасывающей гидролинии будут

                                                                                                          (4.10)

где  Δр_тр.вс - потери давления на трение по длине всасывающей гидро­линии, Па;

        Δр_шт  - потери давления в штуцерном соединении всасывающей гидро­линии с насосом, Па.

Определение численных значений этих потерь давления выполняется при помощи формул (4.7) и (4.8)

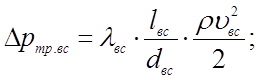                                                                                                   (4.11)

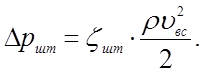                                                                                                            (4.12)

С учетом формул (4.1 1) и (4.12) уравнение (4.9) может быть представлено

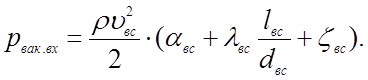                                                                               (4.13)

Для масла АМГ-10 при температуре 50 °С ρ= 850 кг/м³ - с. 241, прило­жение 1 в [19].

Коэффициент Кориолиса α_вс и коэффициент трения λ_вс зависят от числа Рейнольдса (Re_вс=9549 -см. п. 3.6).

Для турбулентого течения (с. 84 в [18]) коэффициент Кориолиса примерно равен 1,1, а коэффициент трения λ зависит от числа Рейнольдса и от относительной эквивалентной шероховатости внутренней поверхности трубы  и вычисляется по формуле Альтшуля (1.102) из [19], с.90:

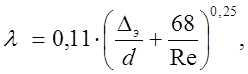
где - эквивалентная шероховатость гидролиний. Для высококачественных безшовных стальных                     труб =0,06 мм;

       d – диаметр трубы всасывающей гидролинии.

Таким образом

α_вс=1,1;

 

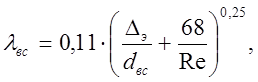
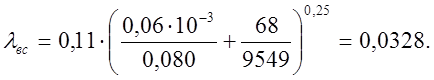
В [7] на с. 8, а также на с. 7 настоящих методических указаний задан ко­эффициент сопротивления одного штуцера ζ_шт=0,6.

Согласно уравнению (4. 13)

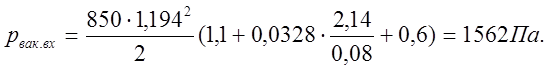
Потери давления во всасывающей гидролинии, вычисленные по формулам (4.11 ) и (4.12) и уравнению (4.10), будут такими

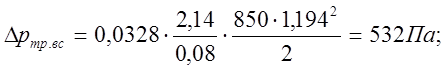
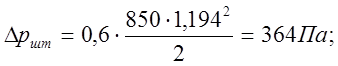
4.6 Определив избыточное давление на входе в насос р_вак.вх, воспользуемся формулой (4.5) для вычисления избыточного давления на выходе из него

р_вых=  - 1562 = 2498438 Па.