Строение механизмов, основные понятия и определения, страница 8

р₃ - число трехподвижных пар, р₄ – число четырехподвижных пар,

p₅ – число пятипожвижных пар.

Механизмы, траектория точек звеньев которых, расположены в одной или параллельных плоскостях называются плоскими. В техники такие механизмы нашли наиболее широкое применение.

На плоскости свободное тело (звено) имеет три степени, свободы, соответ­ственно n свободных звеньев - 3 n степеней свободы. Если конструировать плоскую кинематическую цепь из n звеньев с числом одноподвижных пар р₁ и двухподвижных р₂, то общее число условий связи S = 2 p₁ + p₂ , поскольку одна одноподвижная пара при плоском движении наложит два условия связи, а двухподвижная - одну.

(Формула Чебышева).

Можно доказать, что в плоском механизме одноподвижные кинематический пары являются низшими, а двухподвижные - высшими. Тогда формула Чебышева примет вид: ,

где р_Н и р_В - соответственно число пар низших и высших.

В состав плоского механизма не могут входить трех-, четырех- и пятиподвижные пары, поскольку движение каждого звена ограничено в этом случае наложением трех общих условий связи.

1.5. Строение плоских механизмов по Л. В. АССУРУ

Профессор Л. В. Ассур в 1914-1918 гг. сформулировал принципы создания и исследования плоских рычажных механизмов с низшими парами.

Основная идея Л.В. Ассура состоит в том, что любой плоский механизм может быть создан путем присоединения к начальному звену (или началь­ным звеньям) и стойке кинематических цепей нулевой подвижности, назы­ваемых структурными группами (группами Ассура).

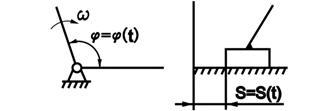
По классификации И. И Артобо-левского начальное звено и стойка, образующие одноподвижную кинематическую, являются механизмом 1-ого класса (рис. 1.4).