Механические свойства алмазоподобных покрытий с подслоем титана определяем на микротвердомере ПМТ-3 согласно методик , изложенных во второй главе . Расчеты велись используя формулы (3) и (5) , согласно которых мы можем расчитать восстановленную микротвердость Н и характеристический параметр оценки адгезионной прочности. Так как мы исследовали образцы с различными толщинами подслоя титана и образцы с различным временем нанесения алмазоподобного покрытия и толщиной титаного подслоя d=65 нм, что дала возможность сделать выводы по выполненной работе. А именно, какое влияние оказывают толщина подслоя нитрида титана и увеличение числа импульсов при нанесении покрытия, на механические свойства алмазоподобных покрытий при испытаниях на вдавливание с измерением диагонали остаточного отпечатка. Результаты измерений и расчета приведены в таблице 3 . По данным измерениям нам удалось выявить определенные зависимости адгезионной прочности алмазоподобного покрытия в зависимости от увеличения частоты импульсов. Так как все данные в формулах были измеряемые, то был найден доверительный интервал для значений восстановленной микротвердости Н.
На основании расчитаных величин я смогла построить зависимость микротвердости Н от нагрузки, которую мы прикладывали проводя опыты. на
Рисунок 10 – Графики зависимости восстановленной микротвердости Н от нагрузки , Н= f(Р) .
- подслой титана равен 39 нм ;
- подслой титана равен 52 нм ;
- подслой титана равен 65 нм . основании полученных зависимостей мы смогли подтвердить теоретическое предположение о том, что между второй и третьими стадиями твердость может переходить через минимум, а затем через максимум . данные зависимости представлены на рисунке 10 и рисунке 11 .
Рисунок 11 – Графики зависимости восстановленной микротвердости Н от нагрузки , Н=f(Р).
- подслой титана равен 104 нм ;
- подслой титана равен 130 нм .
Рисунок 12 – Зависимость характеристического параметра от толщины титанового подслоя.
Основной задачей являлось выяснить зависимость характеристического параметра адгезионной прочности от толщины алмазоподобного покрытия. График зависимости =f( ) приведен на рисунке 12 .
Таким образом такой вид кривой можно объяснить следующим образом . Первая часть кривой объясняется образованием дополнительного межфазного подслоя оксида титана (TiO2), который при толщине слоя Ti до 65 нм образовывается в достаточно большом количестве и тем самым оказывает отрицательное влияние на адгезионную прочность покрытия . Во второй части при толщине Ti 104 нм и 130 нм начинают сказываться пластические свойства титана и поэтому внутренний валик для образования трещин герца образовывается больше и быстрее при более толстом подслое титана . А толщина титана равная 65 нм дает возможность достигнуть наиболее высокой адгезионной прочности покрытия .
При статичесткой обработке результатов мы рассчитали что, среднее арифметическое отклонение экспериментальных данных а1 , а2 , а3 , … , аn , при прямых измерениях равно :
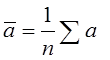 ,
( )
,
( )
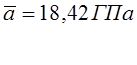
Отклонение каждого из n измерений от среднего
арифметического ![]() оценивали
средней кубической погрешностью:
оценивали
средней кубической погрешностью:
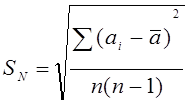 ,
( )
,
( )
S1=0,65 ГПа ;
S2=0,65 ГПа ;
S3=2,97 ГПа ;
S4=1,3 ГПа ;
S5=0,65 ГПа.
Тогда среднее квадратичное отклонение можно определить из выражения:
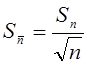 .
( )
.
( )
C учетом надежности (Р=0,95) и числа измерений мы определим коэффициент Стьюдента ta , вычислим доверительный интервал :
а= Sn ta , ( )
а=0,76 2,75=2,01 Гпа .
Тогда искомую величину можно записать а=(18,42![]() 2,01) ГПа .
2,01) ГПа .
Относительная погрешность в этом случае равна:
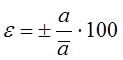 % ,
( )
% ,
( )
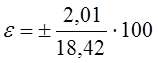 %=
%=![]() % .
% .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.