Типовые звенья в устройствах цифровой обработки сигналов. Цифровые фильтры

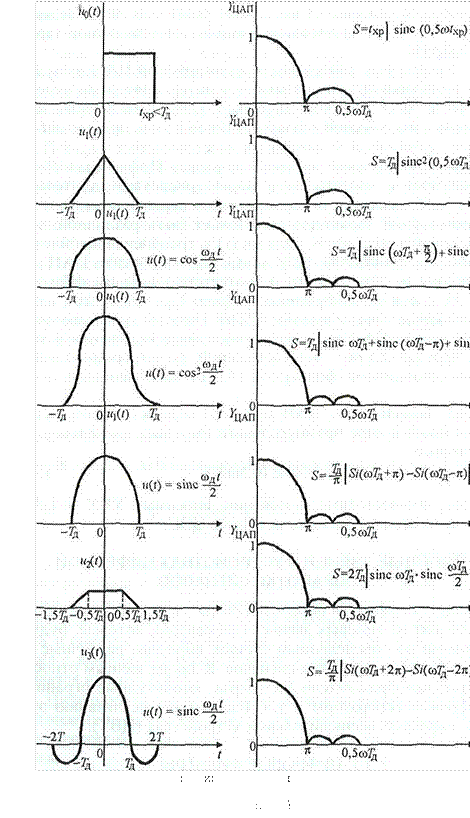S—txp sinc

виях указанные эффекты можно существенно ослабить, поэтому описываемые ниже цифровые фильтры будем считать линейными.

Нерекурсивными называются фильтры без обратных связей

(см. 3.12), работа которых задается разностным уравнением У(п) = Е Вт х(п— т), (7.9)

где х(п),у(п) — цифровые входной и выходной сигналы; Вт — коэффициенты; п — номер отсчета; т — задержка; АШ— порядок фильтра.

Структурные схемы рекурсивного цифрового фильтра в прямой форме (а) и в канонической форме (б) представлены на рис. 7.7. Схема нерекурсивного фильтра получается как частный случай из схемы на рис. 7.7, а, если в ней все коэффициенты равны нулю, т.е. нет обратных связей.

Для описания свойств нерекурсивных фильтров широко используется аппарат Преобразований, позволяющий от разностных уравнений перейти к алгебраическим [З]. Для этого вводится понятие функции передачи цифровых фильтров, которая получила название системной функции H(z). Она равна отношению Спреобразований Y(z) и X(z) от сигналов уф) и х(п) и связана с коэффициентами фильтра следующим соотношением

                                    не) -                           (7.10)

Связь между (7.9) и (7.10) легко устанавливается из двух свойств Преобразования — линейности и смещения во времени. Из H(z) можно получить выражение для комплексного коэффициента передачи фильтра К(ј0) при гармоническом воздействии на его входе в установившемся режиме. Для этого в (7.10) сделаем замену

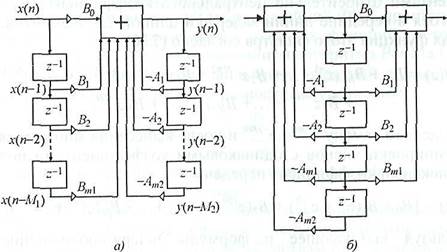
Рис. 77

                                                                               (7.11)

где 0 = отд — нормированная к частоте дискретизации частота входного сигнала. Подставим (7.11) в (7.10) и получим выражение для комплексного коэффициента передачи нерекурсивного фильтра

К(ј0)= ЕВ е-Јто(7.12)

Применяя формулу е—Јто _— cos то —ј sin тэ, представим К(ј0) как сумму действительной и мнимой частей:

                           Евт sin то.                 (7.13)

Модуль К(јб) описывает амплитудно-частотную характеристику фильтра

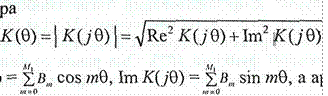(7.14) где Re К(ј0) = ЕВ„, cos то, Im К(ј0) = sin тб, а аргумент К(ј0) описывает фазо частотную характеристику фильтра

Imk(j0)

(Р(О) = Arg КО 0) = arctg(7.15)

Наибольший практический интерес представляют нерекурсивные фильтры с линейной фазочастотной характеристикой. Коэффициенты таких фильтров должны быть симметричны или антисимметричны относительно середины линии задержки фильтра.

Рассмотрим нерекурсивные фильтры с симметричными коэффициентами относительно центрального коэффициента Во, находящегося в середине линии задержки длиной 2N элементов. Системная функция этого фильтра согласно (7.10)

         не) ¹ +.,.+ вр ^N+² +Bp                           вр ^Л' ¹ +

+B2Z ^{N 2} +...+BN_p-2N-l

Сделаем замену z и после вынесения множителя е-.iN0 и группировки членов с одинаковыми коэффициентами получим комплексный коэффициент передачи

К(јО) = [Во +          +        + В2(е^Р0 + е^м20)       +            +          е-:jN0

Используя вытекающее из формулы Эйлера соотношение е] ^Ф +

+ е-ЈФ = 2 cos (Р, получим

                                                  уст               e-jN0                     (7.16)

 где Со = Во, Ст =

Согласно (7.14) АЧХ фильтра описывается формулой

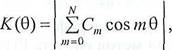           (7.17) а фазочастотная характеристика (ФЧХ) согласно (7.17) формулой

                                       (Р(О) arctg [tg                                       (7.18)

Из 8) следует, что ФЧХ периодически линейна через интервал М) = п Это свойство линейности ФЧХ нерекурсивных фильтров обусловило их широкое применение.

Для нерекурсивного фильтра второго порядка с коэффициентами В, = 1 и имеем 2N=2, 1, тогда из (7.16), (7.17) и (7.18) получим k(j0) = (Во + 2 COS 0)

К(О) = Во + 2 cos 0 1, (Р(О) = arctg [tg (—0)].

Из выражения для следует, что у нерекурсивного фильтра второго порядка существует частота Он, на которой коэффициент передачи = 0. На этой частоте выполняется условие Во + 2 cos Он = 0. Отсюда получим формулу для расчета центрального коэффициента фильтра Во, который определяет частоту Он нулевого коэффициента передачи К(О):

Во 2 COS Он.