Типовые звенья в устройствах цифровой обработки сигналов. Цифровые фильтры, страница 4

Для полного подавления на выходе ПЧ побочных продуктов преобразования ПГ не должен вносить амплитудную и фазовую погрешность в формируемый комплексный сигнал Хе , а КГС

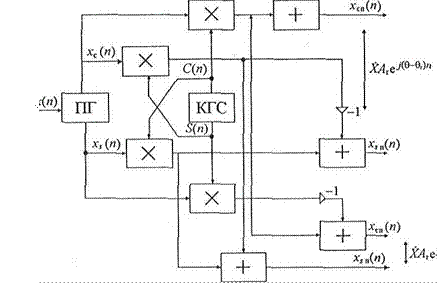
Рис. 7.14

должен формировать абсолютно точные квадратурные компоненты С(п) и S(n). Однако реальные нерекурсивные ПГ вносят амплитудные погрешности, а рекурсивные ПГ — фазовые погрешности, поэтому подавление побочных продуктов происходит не полностью.

7.34. БЛОКИ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ

В ряде устройств цифровой обработки сигналов, например, в амплитудных детекторах, необходимо выполнить операциюу=фЙ В универсальных ЭВМ чаще всего для этих целей применяют итерационную формулу Герона

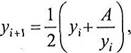
где — результаты вычисления на Ком и i + 1-ом шагах итерации. В качестве начального приближения обычно принимают уо=А.

Пример. А = 0,85. Из формулы Герона приуо= 0,85 получим у, = 0,925; = 0,92195945; уз = 0,92195445.

Точное значение 0,85 = 0,92195444.

Как видно из примера, уже на третьем шаге итерации формула Герона дает практически точный результат. Однако в ней есть операция деления, реализация которой затруднительна в процессорах цифровой обработки сигналов.

Для диапазона значений  можно воспользоваться другой итерационной формулой. Для этого выражение должно бытк представлено в виде СА = a-Fb. Тогда

Yi+l

Нулевое приближение уо определяется из формул Понселе  а] а l+[31 b l a l > l b l

                               (1l b l+ Pl a l   a l < l b

где а = 0,96046, р- 0,39783.

Пример. А = 0,85 = 0,6 + 0,25. Тогда у, = 0,8724256; = 0,916862; уз = 0,921514; у— 0,921922; у— 0,921952;

                            0,9219542;          0,92195443.

Точное значение 0,92195444. Как видно из этого примера, практически точный результат получился лишь на седьмом шаге итерации. Более экономного по программным затратам вычисления корня квадратного можно достичь, если представить отрезок функции у в виде степенного полинома

                       у = ао + щ х +       + азх^з + ... = Е акхК                  (725)

Коэффициенты полинома можно найти различными методами (методом наименьших квадратов, разложением по биному Ньютона, методом экономизации по Чебышеву и т.д.).

Представим функцию у = 6 полиномом второго порядка в удобном для вычислений на процессоре виде

Если задать диапазон изменения числа х в интервале S х 0,4, то полученные методом наименьших квадратов коэффициенты

= 0,1736; щ = 0,5491.

Расчеты показывают, что наибольшая относительная погрешность вычисления функции у = Е по этой формуле в интервале изменения х от 0,1 до 0,4 не превышает 1,33 94. С расширением интервала изменения х погрешность возрастает. Для ее уменьшения можно увеличивать степень полинома или применить процедуру вычислений с условными переходами. Идея ее состоит в следующем. Сравнительно небольшой по изменению аргумента х(х, S х <х2) отрезок функции у представляется степенным полиномом с найденными каким-либо способом коэффициентами щ. Затем входное число х сравнивается с числами х, и х2, причем 211, где п = 1, 2, и определяется положение числа х на числовой оси относительно этих чисел. Далее число х умножается на такое известное число чтобы выполнилось условие

                                                                               (7.26)

где х], х2 — границы изменения аргумента функции у = Е, представленной полиномом (7.25). После этого вычисляется значение у при аргументе и результат умножается на число 2 так как 2 ² '¹ х .2+'^{1 2} =6.

Поясним это примером. Пусть х, = 0,25; м = 0,5, а входное число х 0,01. Чтобы произведение 2²”х попало в интервал 0,25...0,50, умножим число х = 0,0] на 2 ⁵ и получим новое значение аргумента х = (),01•2 ⁵ = 0,32. Затем при х = 0,32 вычислим у = 0,5669 и, умножив его на число 2= 0,1767767, получим 4$5

результат 0, 1002. Точное значение 0,01 =    лишь на 0,2 % отличается от полученного результата.